��Ŀ����
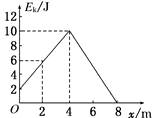
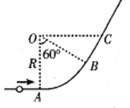
����Ŀ����ͼ��ʾ�ľ�Եϸ�˹���̶�����ֱ���ڣ��뾶ΪR��1/6Բ���θ���ˮƽ�θ˺ʹֲ���б�θ˷ֱ���A��B�������У�Բ���˵�Բ��O���̶���һ��������ĵ��ɡ�����һ����Ϊm����Ϊ�ʵ�Ĵ�����С����ˮƽ���ϣ��Է���ˮƽ���ҡ���С����![]() ���ٶ�ͨ��A�㣬С���ܹ��ϻ�����ߵ�ΪC������C��С���ظ˷��ء�����COB=30����С���һ�ι�A���˲���Բ��ϸ�����µĵ�����СΪ
���ٶ�ͨ��A�㣬С���ܹ��ϻ�����ߵ�ΪC������C��С���ظ˷��ء�����COB=30����С���һ�ι�A���˲���Բ��ϸ�����µĵ�����СΪ![]() ����A��CС��˷����������Ĺ�Ϊ
����A��CС��˷����������Ĺ�Ϊ![]() ���������ٶ�Ϊg����
���������ٶ�Ϊg����
(1)С���һ�ε���B��ʱ�Ķ��ܣ�
(2)С����C���ܵ��Ŀ�������С��
(3)С��A��ǰ˲���Բ���˵ĵ������������m��g��R��ʾ��
���𰸡���1��![]() ��2��
��2��![]() ��3��
��3�� ![]()
������������������ɶ��ܶ������С���һ�ε���B��ʱ�Ķ��ܣ�С���һ�ι�A���˲�䣬��ţ�ٵڶ����ɺͿ��ض�����ʽ���ɼ��ι�ϵ�õ�OC��ľ��룬���ɿ��ض�����С����C���ܵ��Ŀ�������С���ɶ��ܶ������С��A��ǰ˲����ٶȣ���ţ���˶����ɺ���������ʽ���С��A��ǰ˲���Բ���˵ĵ�����
��1��С���A�˶���B��AB����Ϊ���Ƶ㣬���Ե糡�����������ɶ��ܶ����ã� ![]()
�������ݽ�ã� ![]()
��2��С���һ�ι�Aʱ����ţ�ٵڶ����ɵã� ![]()
�����֪�� ![]()
�������������ݽ�ã� ![]()
�ɼ��ι�ϵ�ã�OC��ľ���Ϊ�� ![]()
С����C���ܵ��Ŀ�������С �� 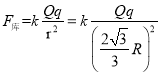
�������![]()
��3����A��C���ɶ��ܶ����ã� ![]()
��C��A���ɶ��ܶ����ã� ![]()
�����֪�� ![]()
С��A��ʱ����ϸ�˶���ĵ����������ϣ���СΪN�䣬��ţ�ٵڶ����ɵã� ![]()
�������Ͻ�ã� 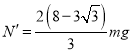 ������ţ�ٵ������ɵã�С��A��ʱ����Բ���˵ĵ�����СΪ
������ţ�ٵ������ɵã�С��A��ʱ����Բ���˵ĵ�����СΪ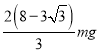 ���������£�
���������£�

 ���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д�
���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д�