题目内容
14. 图示为抚顺某儿童娱乐场的滑道示意图,其中AB为曲面滑道,BC为水平滑道,水平滑道BC与半径为1.25m的$\frac{1}{4}$圆弧滑道CD相切于C点,DE为放在水平地面上的海绵垫.某人从滑道顶端滑下,经过高度差为6m的A点和B点时的速度大小分别为2m/s和6m/s,在C点恰好做平抛运动,最后落在海绵垫上的E点.人的质量为60kg,在BC段的动摩擦因数为0.5.取g=m/s2.问:
图示为抚顺某儿童娱乐场的滑道示意图,其中AB为曲面滑道,BC为水平滑道,水平滑道BC与半径为1.25m的$\frac{1}{4}$圆弧滑道CD相切于C点,DE为放在水平地面上的海绵垫.某人从滑道顶端滑下,经过高度差为6m的A点和B点时的速度大小分别为2m/s和6m/s,在C点恰好做平抛运动,最后落在海绵垫上的E点.人的质量为60kg,在BC段的动摩擦因数为0.5.取g=m/s2.问:(1)从A到B的过程中,人克服阻力做的功是多少?
(2)BC段的长度是多少?
(3)DE段的长度是多少?
分析 (1)对A到B的过程运用动能定理,根据动能定理求出人克服阻力做的功.
(2)当人在C点对轨道的压力为零时,做平抛运动,根据在C点重力提供向心力,求出速度,通过匀变速直线运动的速度位移公式求出BC.
(3)根据平抛运动的高度求出平抛运动的时间,再根据水平速度和时间求出水平位移,DE的长度等于水平位移减去圆弧轨道的半径
解答 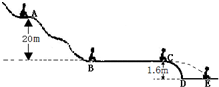 解:(1)由动能定理:${W}_{G}-{W}_{f}=\frac{1}{2}{mv}_{B}^{2}-\frac{1}{2}{mv}_{A}^{2}$
解:(1)由动能定理:${W}_{G}-{W}_{f}=\frac{1}{2}{mv}_{B}^{2}-\frac{1}{2}{mv}_{A}^{2}$
得:Wf=2640J
(2)BC段加速度为:a=μg=5m/s2
设在C点的最小速度为vm,则在C点由$mg=\frac{{mv}_{m}^{2}}{r}$
解得${v}_{m}=\sqrt{gr}=\frac{5\sqrt{2}}{2}m/s$
由${v}_{B}^{2}{-v}_{m}^{2}=2a{x}_{BC}$
联立解得xBC=2.35m
(3)在平抛阶段
R=$\frac{1}{2}g{t}^{2}$
xDE=vmt-R
联理解得xDE=0.52m
答:(1)从A到B的过程中,人克服阻力做的功是2640J
(2)BC段的长度是2.35m
(3)DE段的长度是0.52m
点评 本题是多过程问题,关键是理清运动过程,选择合适的规律,比如牛顿运动定律、动能定理进行求解

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.一点电荷从电场中的a点移到b点时,电场力做功为零,则( )
| A. | a、b两点的场强一定相等 | B. | 一定沿等势面移动 | ||
| C. | 电势能的变化为零 | D. | a、b两点电势一定相等 |
5.用电动势为E、内阻为r的电源对外电路供电,下列判断中正确的是( )
①电源短路时,路端电压为零,电路电流达最大值
②外电路断开时,电路电压为零,路端电压也为零
③路端电压增大时,流过电源的电流一定减小
④路端电压增大时,电源的效率一定增大
①电源短路时,路端电压为零,电路电流达最大值
②外电路断开时,电路电压为零,路端电压也为零
③路端电压增大时,流过电源的电流一定减小
④路端电压增大时,电源的效率一定增大
| A. | ① | B. | ①③ | C. | ②④ | D. | ①③④ |
2.某公路上发生了一起交通事故,一辆总质量大于12t的载重汽车与一辆总质量小于3.5t的小型汽车迎面相撞,交警勘察得知两车制动时的速度分别是15m/s和25m/s,并测得两车制动点间的距离是116.25m,事故地点距载重汽车制动点的距离是36.25m,如图所示.已知载重汽车制动时间加速度是0.4m/s2,小型汽车制动时的加速度是0.6m/s2,两车长度忽略,看作质点作匀变速运动.则可分析得出( )

| A. | 两车相撞时载重汽车的速度是13m/s | |
| B. | 两车相撞时小型汽车的速度是22m/s | |
| C. | 小型汽车制动过程的平均速度是24m/s | |
| D. | 两司机是同时制动刹车的 |
4.关于第一宇宙速度,下列说法中正确的是( )
| A. | 第一宇宙速度是人造卫星绕地球做匀速圆周运动的最小速度 | |
| B. | 第一宇宙速度是人造卫星绕地球做匀速圆周运动的最大速度 | |
| C. | 第一宇宙速度是地球同步卫星的运行速度 | |
| D. | 不同行星的第一宇宙速度是相同的 |

 在做“研究匀变速直线运动”的实验时,得到一条纸带如图所示,A、B、C、D、E、F、G为计数点,每两个计数点间还有4个点未画出,x1=1.20cm,x2=1.60cm,x3=2.00cm,x4=2.40cm,x5=2.80cm,x6=3.20cm
在做“研究匀变速直线运动”的实验时,得到一条纸带如图所示,A、B、C、D、E、F、G为计数点,每两个计数点间还有4个点未画出,x1=1.20cm,x2=1.60cm,x3=2.00cm,x4=2.40cm,x5=2.80cm,x6=3.20cm 如图所示,一质量m=4.0kg的物体,由高h=2.0m、倾角θ=53°的固定斜面顶端滑到底端.物体与斜面间的动摩擦因数为μ=0.2.求;
如图所示,一质量m=4.0kg的物体,由高h=2.0m、倾角θ=53°的固定斜面顶端滑到底端.物体与斜面间的动摩擦因数为μ=0.2.求;