题目内容
2.某公路上发生了一起交通事故,一辆总质量大于12t的载重汽车与一辆总质量小于3.5t的小型汽车迎面相撞,交警勘察得知两车制动时的速度分别是15m/s和25m/s,并测得两车制动点间的距离是116.25m,事故地点距载重汽车制动点的距离是36.25m,如图所示.已知载重汽车制动时间加速度是0.4m/s2,小型汽车制动时的加速度是0.6m/s2,两车长度忽略,看作质点作匀变速运动.则可分析得出( )
| A. | 两车相撞时载重汽车的速度是13m/s | |
| B. | 两车相撞时小型汽车的速度是22m/s | |
| C. | 小型汽车制动过程的平均速度是24m/s | |
| D. | 两司机是同时制动刹车的 |
分析 根据匀变速直线运动的速度位移关系由初速度、位移及加速度分析相撞时的末速度,再由平均速度公式求平均速度.
解答 解:A、由题意知,载重汽车的初速度v0=15m/s,刹车时的加速度a=-0.4m/s2,位移x=36.25m
据速度位移关系有${v}^{2}-{v}_{0}^{2}=2ax$可得相撞时的速度v=$\sqrt{{v}_{0}^{2}+2ax}=\sqrt{1{5}^{2}+2×(-0.4)×36.25}m/s$=14m/s,故A错误;
B、小型汽车的初速度v0′=25m/s,刹车时的加速度a′=-0.6m/s2,位移x′=116.25-36.26m=80m
据速度位移关系知相撞前的末速度$v′=\sqrt{{v}_{0}^{′2}+2a′x′}=\sqrt{2{5}^{2}+2×(-0.6)×80}$m/s=23m/s,故B错误;
C、由B分析知,小型汽车制动过程中的平均速度$\overline{v}=\frac{{v}_{0}^{′}+v′}{2}=\frac{25+23}{2}m/s=24m/s$,故C正确;
D、载重汽车的减速时间t=$\frac{v-{v}_{0}}{a}=\frac{14-15}{-0.4}s=2.5s$,小型汽车减速时间t$′=\frac{v′-{v}_{0}′}{a′}=\frac{23-25}{-0.6}s=3.3s$,可见两司机不是同时刹车的,故D错误.
故选:C.
点评 掌握匀变速直线运动的速度位移关系及速度时间关系是正确解题的关键,不难属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.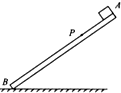 如图所示,平直木板AB倾斜放置,板上的P点距A端较近,小物块与木板间的动摩擦因数由A到B逐渐减小.先让物块从A由静止开始滑到B.然后,将A着地,抬高B,使木板的倾角与前一过程相同,再让物块从B由静止开始滑到A.上述两过程相比较,下列说法中一定正确的有( )
如图所示,平直木板AB倾斜放置,板上的P点距A端较近,小物块与木板间的动摩擦因数由A到B逐渐减小.先让物块从A由静止开始滑到B.然后,将A着地,抬高B,使木板的倾角与前一过程相同,再让物块从B由静止开始滑到A.上述两过程相比较,下列说法中一定正确的有( )
 如图所示,平直木板AB倾斜放置,板上的P点距A端较近,小物块与木板间的动摩擦因数由A到B逐渐减小.先让物块从A由静止开始滑到B.然后,将A着地,抬高B,使木板的倾角与前一过程相同,再让物块从B由静止开始滑到A.上述两过程相比较,下列说法中一定正确的有( )
如图所示,平直木板AB倾斜放置,板上的P点距A端较近,小物块与木板间的动摩擦因数由A到B逐渐减小.先让物块从A由静止开始滑到B.然后,将A着地,抬高B,使木板的倾角与前一过程相同,再让物块从B由静止开始滑到A.上述两过程相比较,下列说法中一定正确的有( )| A. | 物块经过P点的动能,前一过程较大 | |
| B. | 物块从顶端滑到P点的过程中因摩擦产生的热量,前一过程较少 | |
| C. | 物块滑到底端的速度大小,两个过程一样大 | |
| D. | 物块从顶端滑到底端的时间,前一过程较长 |
5.一个质子以1.0×107m/s的速度撞入一个静止的铝(${\;}_{13}^{27}$Al)原子核后被俘获,铝原子核变为硅(${\;}_{14}^{28}$Si)原子核,则下列判断中正确的是( )
| A. | 核反应方程为${\;}_{13}^{27}$Al+${\;}_1^1$H→${\;}_{14}^{28}$Si | |
| B. | 核反应方程为${\;}_{13}^{27}$Al+${\;}_0^1$n→${\;}_{14}^{28}$Si | |
| C. | 硅原子核速度的数量级为107m/s,方向跟质子的初速度方向一致 | |
| D. | 硅原子核速度的数量级为105m/s,方向跟质子的初速度方向一致 |
11.下列说法正确的是( )
| A. | 瞬时速度可以看成时间趋于无穷小时的平均速度 | |
| B. | 做变速运动的物体在某段时间内的平均速度,一定和物体在这段时间内各个时刻的瞬时速度大小的平均值相等 | |
| C. | 有时速度的正负表示大小,所以-5 m/s<3 m/s | |
| D. | 物体做变速运动时,平均速度是指物体通过的路程与所用时间的比值 |
12.关于速度,速度变化量,加速度,下列说法中正确的是( )
| A. | 物体运动时,速度的变化量越大,它的加速度越大 | |
| B. | 某时刻物体的速度为零,其加速度不可能很大 | |
| C. | 速度很大的物体,其加速度可能为零 | |
| D. | 运动物体的速度方向向东,其加速度方向不可能向西 |

 如图所示为一传送带的模型,传送带水平部分AB长度L在0.5m≤L≤2.0m的范围内取值,AB距水平地面的高度h=0.45m,皮带轮顺时针匀速转动使传送带总保持v=2.0m/s的速度匀速运动.现将一工件(可视为质点)从静止轻放在A端,一段时间后工件运动到B端并从B端水平抛出,已知工件与皮带之间的动摩擦因数μ=0.20,g取10m/s2.
如图所示为一传送带的模型,传送带水平部分AB长度L在0.5m≤L≤2.0m的范围内取值,AB距水平地面的高度h=0.45m,皮带轮顺时针匀速转动使传送带总保持v=2.0m/s的速度匀速运动.现将一工件(可视为质点)从静止轻放在A端,一段时间后工件运动到B端并从B端水平抛出,已知工件与皮带之间的动摩擦因数μ=0.20,g取10m/s2.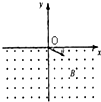 如图,在y<0的区域内存在匀强磁场,磁场方向垂直于xOy平面并指向纸面外,磁感应强度为B,一不计重力带正电的粒子以速度v0从O点射入磁场,入射方向在xOy平面内且与x轴正向的夹角为θ.若粒子射出磁场的位置与O点距离为L,求:
如图,在y<0的区域内存在匀强磁场,磁场方向垂直于xOy平面并指向纸面外,磁感应强度为B,一不计重力带正电的粒子以速度v0从O点射入磁场,入射方向在xOy平面内且与x轴正向的夹角为θ.若粒子射出磁场的位置与O点距离为L,求: 图示为抚顺某儿童娱乐场的滑道示意图,其中AB为曲面滑道,BC为水平滑道,水平滑道BC与半径为1.25m的$\frac{1}{4}$圆弧滑道CD相切于C点,DE为放在水平地面上的海绵垫.某人从滑道顶端滑下,经过高度差为6m的A点和B点时的速度大小分别为2m/s和6m/s,在C点恰好做平抛运动,最后落在海绵垫上的E点.人的质量为60kg,在BC段的动摩擦因数为0.5.取g=m/s2.问:
图示为抚顺某儿童娱乐场的滑道示意图,其中AB为曲面滑道,BC为水平滑道,水平滑道BC与半径为1.25m的$\frac{1}{4}$圆弧滑道CD相切于C点,DE为放在水平地面上的海绵垫.某人从滑道顶端滑下,经过高度差为6m的A点和B点时的速度大小分别为2m/s和6m/s,在C点恰好做平抛运动,最后落在海绵垫上的E点.人的质量为60kg,在BC段的动摩擦因数为0.5.取g=m/s2.问: