题目内容
19.在用单摆测重力加速度的实验中,某同学利用两个单摆测得其周期分别为T1、T2,已知两个单摆的摆长之和为L,则测得当地重力加速的表达式为$\frac{4{π}^{2}L}{{T}_{1}^{2}+{T}_{2}^{2}}$.分析 根据单摆的周期公式T=2π$\sqrt{\frac{L}{g}}$,对两个单摆分别列式,再化简求解即可.
解答 解:根据单摆的周期公式T=2π$\sqrt{\frac{L}{g}}$,得:
T1=2$π\sqrt{\frac{{L}_{1}}{g}}$
T2=2π$\sqrt{\frac{{L}_{2}}{g}}$
据题有:L1+L2=L.
联立以上各式解得 g=$\frac{4{π}^{2}L}{{T}_{1}^{2}+{T}_{2}^{2}}$
故答案为:$\frac{4{π}^{2}L}{{T}_{1}^{2}+{T}_{2}^{2}}$.
点评 解决本题的关键要明确实验原理:单摆的周期公式T=2π$\sqrt{\frac{L}{g}}$,应用单摆周期公式即可正确解答.

练习册系列答案
相关题目
1.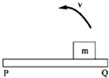 如图所示,粗糙木板PQ,其Q端放有质量为m的滑块.当木板以p端为轴,缓慢地由水平转至竖直的过程中,滑块受支持力N,摩擦力f的情况是( )
如图所示,粗糙木板PQ,其Q端放有质量为m的滑块.当木板以p端为轴,缓慢地由水平转至竖直的过程中,滑块受支持力N,摩擦力f的情况是( )
 如图所示,粗糙木板PQ,其Q端放有质量为m的滑块.当木板以p端为轴,缓慢地由水平转至竖直的过程中,滑块受支持力N,摩擦力f的情况是( )
如图所示,粗糙木板PQ,其Q端放有质量为m的滑块.当木板以p端为轴,缓慢地由水平转至竖直的过程中,滑块受支持力N,摩擦力f的情况是( )| A. | N一直减小 | B. | f一直减小 | C. | f一直增大 | D. | f减小先后增大 |
4. 如图所示,两个等量的正电荷分别置于P、Q两位置,在P、Q连线的垂直平分线上有M、N两点,另有一试探电荷q,则( )
如图所示,两个等量的正电荷分别置于P、Q两位置,在P、Q连线的垂直平分线上有M、N两点,另有一试探电荷q,则( )
 如图所示,两个等量的正电荷分别置于P、Q两位置,在P、Q连线的垂直平分线上有M、N两点,另有一试探电荷q,则( )
如图所示,两个等量的正电荷分别置于P、Q两位置,在P、Q连线的垂直平分线上有M、N两点,另有一试探电荷q,则( )| A. | 若q是正电荷,q在N点的电势能比在M点的电势能大 | |
| B. | 若q是负电荷,q在M点的电势能比在N点的电势能大 | |
| C. | M、N两点的电场强度方向向右 | |
| D. | 中垂线MN为一条等势线 |
11.下列说法正确的是( )
| A. | 瞬时速度可以看成时间趋于无穷小时的平均速度 | |
| B. | 做变速运动的物体在某段时间内的平均速度,一定和物体在这段时间内各个时刻的瞬时速度大小的平均值相等 | |
| C. | 有时速度的正负表示大小,所以-5 m/s<3 m/s | |
| D. | 物体做变速运动时,平均速度是指物体通过的路程与所用时间的比值 |
8.赵凯华教授说过“加速度是人类认识史上最难建立的概念之一,也是每个初学物理的人最不易真正掌握的概念…”.所以对加速度的认识易出现错误.下列说法中错误的是( )
| A. | 加速度是描述速度变化快慢的物理量,速度大,加速度不一定大 | |
| B. | 速度变化得越快,加速度就越大 | |
| C. | 速度变化的方向为正,加速度的方向就为负 | |
| D. | 加速度可能既不与速度同向,也不与速度反向 |
9.一物体在桌面上滑行,受到摩擦力作用,其大小为F,则( )
| A. | 桌面也受到摩擦力作用,大小为F,方向和物体运动方向一致 | |
| B. | 桌面也受到摩擦力作用,大小为F,方向和物体运动方向相反 | |
| C. | 桌面也受到摩擦力作用,大小不等于F | |
| D. | 桌面不受摩擦力作用 |

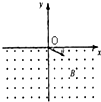 如图,在y<0的区域内存在匀强磁场,磁场方向垂直于xOy平面并指向纸面外,磁感应强度为B,一不计重力带正电的粒子以速度v0从O点射入磁场,入射方向在xOy平面内且与x轴正向的夹角为θ.若粒子射出磁场的位置与O点距离为L,求:
如图,在y<0的区域内存在匀强磁场,磁场方向垂直于xOy平面并指向纸面外,磁感应强度为B,一不计重力带正电的粒子以速度v0从O点射入磁场,入射方向在xOy平面内且与x轴正向的夹角为θ.若粒子射出磁场的位置与O点距离为L,求: 图示为抚顺某儿童娱乐场的滑道示意图,其中AB为曲面滑道,BC为水平滑道,水平滑道BC与半径为1.25m的$\frac{1}{4}$圆弧滑道CD相切于C点,DE为放在水平地面上的海绵垫.某人从滑道顶端滑下,经过高度差为6m的A点和B点时的速度大小分别为2m/s和6m/s,在C点恰好做平抛运动,最后落在海绵垫上的E点.人的质量为60kg,在BC段的动摩擦因数为0.5.取g=m/s2.问:
图示为抚顺某儿童娱乐场的滑道示意图,其中AB为曲面滑道,BC为水平滑道,水平滑道BC与半径为1.25m的$\frac{1}{4}$圆弧滑道CD相切于C点,DE为放在水平地面上的海绵垫.某人从滑道顶端滑下,经过高度差为6m的A点和B点时的速度大小分别为2m/s和6m/s,在C点恰好做平抛运动,最后落在海绵垫上的E点.人的质量为60kg,在BC段的动摩擦因数为0.5.取g=m/s2.问: