��Ŀ����
3������Ϊ4m��С���A��ֹ��������h��ˮƽ����ı�Ե������Ϊm��С���B��������A�˶����ٶ�v0=3L$\sqrt{\frac{g}{2h}}$��֮������������ײʱ�伫�̣�������A�뿪���棬����ص���������ˮƽ����ΪL������B�����˶�����֪B�������Ķ�Ħ������Ϊ�̣��������ٶ�Ϊg������1��B���˵ľ���Ϊ���٣�
��2�������˶������У����B�˷�Ħ�������Ĺ�������ײ��ʧ�Ļ�е��֮��Ϊ���٣�
���� ��1��С���B�����A���������Ĺ��̣����ض����غ㶨�ɣ�����A�뿪������ƽ���˶����ɸ߶�h��ˮƽ����ΪL�������A���ٶȣ����ݶ����غ㶨�����B������ٶȣ����ݶ��ܶ������B���˵ľ��룮
��2�����B�˷�Ħ�������Ĺ�������ʧ�Ķ��ܣ��ɶ��ܵļ��㹫ʽ���������ײ��ʧ�Ļ�е�ܣ�Ȼ�������ֵ���ɣ�
��� �⣺��tΪA���뿪��������ؾ�����ʱ�䣬V��ʾ������A���ٶȣ��У�
h=$\frac{1}{2}$gt2
L=vAt
��ã�vA=L$\sqrt{\frac{g}{2h}}$
��vΪ������B���ٶȵĴ�С���ɶ����غ㶨�ɵã�
mv0=MvA-mv
�ɹ��ܹ�ϵ�ã�$��E=\frac{1}{2}m{v}_{0}^{2}-\frac{1}{2}��4m{v}_{A}^{2}-\frac{1}{2}m{v}^{2}$
��B���˵ľ���Ϊl���ɶ��ܶ����ã�
-��mgx=0-$\frac{1}{2}$mv2
�����ϸ�ʽ�ã�x=$\frac{{L}^{2}}{4��h}$
��2�����B�˷�Ħ�������Ĺ�����B��ʧ�Ķ��ܣ��ã�
$\frac{{W}_{f}}{��E}=\frac{\frac{1}{2}m{v}^{2}}{��E}$
�������ݵã�$\frac{{W}_{f}}{��E}=\frac{1}{4}$
�𣺣�1��B���˵ľ���Ϊ$\frac{{L}^{2}}{4��h}$��
��2�������˶������У����B�˷�Ħ�������Ĺ�������ײ��ʧ�Ļ�е��֮��Ϊ$\frac{1}{4}$��
���� �����Ƕ���̵����⣬��������������̡�ѡ�������ɵ�������������ײ����������Ĺ����Ƕ����غ㣮����ƽ���˶���֪���߶Ⱥ�ˮƽ����������ƽ���˶��ij��ٶȣ�

 ��ͼ��ʾ��һ����ΪM��б���徲ֹ��ˮƽ�����ϣ�����B����б�����ϵ���F��������б�������ϻ���A��B֮��Ķ�Ħ������Ϊ�̣��̣�tan�ȣ���������Ϊm��������
��ͼ��ʾ��һ����ΪM��б���徲ֹ��ˮƽ�����ϣ�����B����б�����ϵ���F��������б�������ϻ���A��B֮��Ķ�Ħ������Ϊ�̣��̣�tan�ȣ���������Ϊm��������| A�� | A��B������Ծ�ֹ | |
| B�� | B��б���Ķ�Ħ������Ϊ$\frac{F-mgsin��-��mgcos��}{2sincos��}$ | |
| C�� | �����б�����Ħ��������Fcos�� | |
| D�� | �����ܵ���ѹ�����ڣ�M+2m��g |
 ��ͼ��ʾ������Ϊm�������ת̨֮������Ħ����Ϊ���������k���������ת��OO�����R�������ת̨�ɾ�ֹ��ʼת������ת�ٻ������ӵ�һ��ֵʱ����鼴����ת̨�ϻ�����������ɾ�ֹ����Ի���ǰ˲��Ĺ����У�ת̨��Ħ������������Ĺ�Ϊ��������
��ͼ��ʾ������Ϊm�������ת̨֮������Ħ����Ϊ���������k���������ת��OO�����R�������ת̨�ɾ�ֹ��ʼת������ת�ٻ������ӵ�һ��ֵʱ����鼴����ת̨�ϻ�����������ɾ�ֹ����Ի���ǰ˲��Ĺ����У�ת̨��Ħ������������Ĺ�Ϊ��������| A�� | 0 | B�� | 2��kmgR | C�� | 2kmgR | D�� | 0.5kmgR |
 ��ͼ��ʾ���������յ�Lλ�ڵ�������������ϣ����ڸõ�������ڵ�������������Ĺ�ͬ�����£���������һ������ͬ�������Ƶ����˶����ݴˣ���ѧ���������������յ�L�����ռ�վ��ʹ��������ͬ�����Ƶ����˶�����v1��T1��a1�ֱ��ʾ�ÿռ�վ�����ٶȡ����ڡ����ļ��ٶȵĴ�С��v2��T2��a2�ֱ��ʾ���������ٶȡ����ڡ����ļ��ٶȵĴ�С����v3��T3��a3�ֱ��ʾ����ͬ���������ٶȡ����ڡ����ļ��ٶȵĴ�С�������ж���ȷ���ǣ�������
��ͼ��ʾ���������յ�Lλ�ڵ�������������ϣ����ڸõ�������ڵ�������������Ĺ�ͬ�����£���������һ������ͬ�������Ƶ����˶����ݴˣ���ѧ���������������յ�L�����ռ�վ��ʹ��������ͬ�����Ƶ����˶�����v1��T1��a1�ֱ��ʾ�ÿռ�վ�����ٶȡ����ڡ����ļ��ٶȵĴ�С��v2��T2��a2�ֱ��ʾ���������ٶȡ����ڡ����ļ��ٶȵĴ�С����v3��T3��a3�ֱ��ʾ����ͬ���������ٶȡ����ڡ����ļ��ٶȵĴ�С�������ж���ȷ���ǣ�������| A�� | v3��v2��v1 | B�� | T3��T2��T1 | C�� | a3��a1��a2 | D�� | a3��a2��a1 |
 ��ͼ��ʾ����Դ�綯��ΪE������Ϊr����ѹ��V1��V2��V3Ϊ�����ѹ����R1��R3Ϊ��ֵ���裬R2Ϊ�������裨����ֵ���¶����߶���С����CΪ���������պϿ���S��������C�е���Aǡ�þ�ֹ�������´�25�����ߵ�35��Ĺ����У�������Դ�ĵ����仯���ǡ�I����ֻ��ѹ����ʾ���仯���ǡ�U1����U2�͡�U3�����ڴ˹����У�������
��ͼ��ʾ����Դ�綯��ΪE������Ϊr����ѹ��V1��V2��V3Ϊ�����ѹ����R1��R3Ϊ��ֵ���裬R2Ϊ�������裨����ֵ���¶����߶���С����CΪ���������պϿ���S��������C�е���Aǡ�þ�ֹ�������´�25�����ߵ�35��Ĺ����У�������Դ�ĵ����仯���ǡ�I����ֻ��ѹ����ʾ���仯���ǡ�U1����U2�͡�U3�����ڴ˹����У�������| A�� | V1ʾ����С | |
| B�� | $\frac{��{U}_{2}}{��I}$��$\frac{��{U}_{3}}{��I}$ | |
| C�� | Q��������� | |
| D�� | R3�еĵ���������M��N����A�ȼ������� |
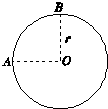 ��ͼ��ʾ��һ�ʵ��ذ뾶Ϊr=40cm��Բ����A���������ʱ���˶�����4s���˶�$\frac{3}{4}$Բ�ܵ���B�㣮��
��ͼ��ʾ��һ�ʵ��ذ뾶Ϊr=40cm��Բ����A���������ʱ���˶�����4s���˶�$\frac{3}{4}$Բ�ܵ���B�㣮�� ��ͼ��ʾ��һ����ΪM=4kg��С����˷���һ����Ϊm=2kg�����飬������v0=6m/s�Ĺ�ͬ�ٶ��ع⻬ˮƽ������ֱǽ�˶�������ǽ��ײ��ʱ�伫�̣�������ײʱ��е�ܵ���ʧ��������С��֮��Ķ�Ħ��������=0.5������L�㹻�������鲻�ᵽ�ﳵ���Ҷˣ�����С����������Ծ�ֹ�������������У�
��ͼ��ʾ��һ����ΪM=4kg��С����˷���һ����Ϊm=2kg�����飬������v0=6m/s�Ĺ�ͬ�ٶ��ع⻬ˮƽ������ֱǽ�˶�������ǽ��ײ��ʱ�伫�̣�������ײʱ��е�ܵ���ʧ��������С��֮��Ķ�Ħ��������=0.5������L�㹻�������鲻�ᵽ�ﳵ���Ҷˣ�����С����������Ծ�ֹ�������������У�