题目内容
10. 如图所示,质量m=1kg的物块放置在足够长的木板OA上,木板与水平面的夹角θ可在0-90°之间变化,作用在物体上的力F=8N,方向始终水平于斜面,已知物块与木板间的动摩擦因数为0.2,假定物块与木板间的最大静摩擦力始终等于滑动摩擦力,重力加速度g取10m/s2,取sin37°=0.6,cos37°=0.8则:
如图所示,质量m=1kg的物块放置在足够长的木板OA上,木板与水平面的夹角θ可在0-90°之间变化,作用在物体上的力F=8N,方向始终水平于斜面,已知物块与木板间的动摩擦因数为0.2,假定物块与木板间的最大静摩擦力始终等于滑动摩擦力,重力加速度g取10m/s2,取sin37°=0.6,cos37°=0.8则:(1)当θ=0和θ=90°时,分别求出物体加速度的大小;
(2)当θ=37°时,物块在F的作用下由静止开始运动,经过5s后撤去力F,求物体沿木板上升到最高点时离出发点的距离;(保留三位有效数字)
(3)当θ在0-90°时之间变化时,试分析物体受到摩擦力大小和方向的变化情况.
分析 (1)利用牛顿第二定律即可求解.(2)利用牛顿运动定律和几何关系即可求解.(3)先找出临界条件,找出关系式,在分析判断摩擦力的变化.
解答 解:(1)当θ=0时,据牛顿第二定律得:F-μmg=ma1
代入数据解得:a1=6m/s2
当θ=90°时,据牛顿第二定律得:mg-F=ma2
代入数据解得:a2=2m/s2
(2)设物体在F的作用加速度为a3,撤去F时的加速度大小为 a4,由牛顿第二定律得:
F-mgsinθ-μmgcosθ=ma3
代入数据解得:a3=0.4m/s2
mgsinθ+μmgcosθ=ma4
代入数据解得:a4=7.6m/s2
设物块在F作用时的位移大小为x1,撤去F时位移大小为x2,据运动学公式得:
${x}_{1}=\frac{1}{2}{a}_{3}{t}^{2}$
代入数据解得:x1=5m
${x}_{2}=\frac{{v}^{2}}{2{a}_{4}}=\frac{({a}_{3}t)^{2}}{2{a}_{4}}$
代入数据解得:x2=0.26m
所以物体沿木板上升到最高点时离出发点的距离:x=5.26m
(3)设物体刚好不能向上滑时木板夹角为θ1,物体不受摩擦力木板夹角为θ2,物体刚好向下滑动木板夹角为θ3,由受力平衡分析可知:
F=mgsinθ1+μmgcosθ1
F=mgsinθ2
F=mgsinθ3-μmgcosθ3
木板夹角由0到θ1过程中,物体受滑动摩擦力,大小不断变小,方向沿木板向下;
木板夹角由θ1到θ2过程中,物体受静摩擦力,大小不断变小,方向沿木板向下;
木板夹角由θ2到θ3过程中,物体受静摩擦力,大小不断变大,方向沿木板向上;
当θ3到90°时之间变化时,物体受滑动摩擦力,大小不断减小,方向沿木板向上.
答:(1)当θ=0和θ=90°时,分别求出物体加速度的大小6m/s2和2m/s2;
(2)当θ=37°时,物块在F的作用下由静止开始运动,经过5s后撤去力F,求物体沿木板上升到最高点时离出发点的距离5.26m;
(3)当θ在0-90°时之间变化时,试分析物体受到摩擦力大小和方向的变化情况:木板夹角由0到θ1过程中,物体受滑动摩擦力,大小不断变小,方向沿木板向下;木板夹角由θ1到θ2过程中,物体受静摩擦力,大小不断变小,方向沿木板向下;木板夹角由θ2到θ3过程中,物体受静摩擦力,大小不断变大,方向沿木板向上;当θ3到90°时之间变化时,物体受滑动摩擦力,大小不断减小,方向沿木板向上.
点评 本题前2问求解方法思路较清晰,但第三问易出错,关键是找出三种临界,即物体不向上运动、不受摩擦力和受滑动摩擦力,再据角度的变化判断摩擦力的变化.

 阅读快车系列答案
阅读快车系列答案 一条足够长的浅色水平传送带自右向左匀速运行,现将一个木炭包无初速地放在传送带的最右端,木炭包在传送带上留下一小段黑色的径迹后平稳运行,下列说法中正确的是( )
一条足够长的浅色水平传送带自右向左匀速运行,现将一个木炭包无初速地放在传送带的最右端,木炭包在传送带上留下一小段黑色的径迹后平稳运行,下列说法中正确的是( )| A. | 黑色的径迹将出现在木炭包的左侧 | |
| B. | 平稳运行时木炭包将受到静摩擦力的作用 | |
| C. | 木炭包的质量越大,径迹的长度越短 | |
| D. | 木炭包与传送带间动摩擦因数越大,径迹的长度越短 |
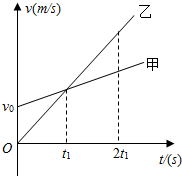
| A. | 甲、乙两车不可能相遇,t1时刻相距最近 | |
| B. | 甲、乙两车只能相遇一次,在相遇前t1时刻距离最远 | |
| C. | 甲、乙两车可能相遇两次,t1时刻相距最远 | |
| D. | 在2t1时刻乙车在甲车前方 |
 如图1所示,竖直光滑杆固定不动,套在杆上的弹簧下端固定,将套在杆上的滑块向下压缩弹簧至离地高度h=0.1m处,滑块与弹簧不拴接.现由静止释放滑块,通过传感器测量到滑块的速度和离地高度h并作出如图2滑块的Ek-h图象,其中高度从0.2m上升到0.35m范围内图象为直线,其余部分为曲线,以地面为零势能面,取g=10m/s2,由图象可知( )
如图1所示,竖直光滑杆固定不动,套在杆上的弹簧下端固定,将套在杆上的滑块向下压缩弹簧至离地高度h=0.1m处,滑块与弹簧不拴接.现由静止释放滑块,通过传感器测量到滑块的速度和离地高度h并作出如图2滑块的Ek-h图象,其中高度从0.2m上升到0.35m范围内图象为直线,其余部分为曲线,以地面为零势能面,取g=10m/s2,由图象可知( )| A. | 小滑块的质量为0.1kg | |
| B. | 轻弹簧原长为0.2m | |
| C. | 弹簧最大弹性势能为0.5J | |
| D. | 小滑块的重力势能与弹簧的弹性势能总和最小为0.4J |
 如图所示,在光滑水平桌面上有一光滑小孔O;一根轻绳穿过小孔,一端连接质量为m=1kg的小球A,另一端连接质量为M=4kg的重物B.小球A沿半径r=0.1m的圆周做匀速圆周运动,则:
如图所示,在光滑水平桌面上有一光滑小孔O;一根轻绳穿过小孔,一端连接质量为m=1kg的小球A,另一端连接质量为M=4kg的重物B.小球A沿半径r=0.1m的圆周做匀速圆周运动,则: 如图所示,一个长为L、质量为M的长方形木块,静止在光滑水平面上,一个质量为m的物块(可视为质点),以水平初速度v0从木块的左端滑向右端,设物块与木块间的动摩擦因数为μ,当物块与木块达到相对静止时,物块仍在长木块上,求系统机械能转化成多少内能Q.
如图所示,一个长为L、质量为M的长方形木块,静止在光滑水平面上,一个质量为m的物块(可视为质点),以水平初速度v0从木块的左端滑向右端,设物块与木块间的动摩擦因数为μ,当物块与木块达到相对静止时,物块仍在长木块上,求系统机械能转化成多少内能Q. 如图所示,木块A的质量mA=1kg,足够长的木板B的质量mB=4kg,质量为mC=2kg的木块C置于木板B上,水平面光滑,B、C之间有摩擦,现使A以vo=10m/s的初速度向右运动,与B碰撞后以立即以4m/s的速度弹回.求:
如图所示,木块A的质量mA=1kg,足够长的木板B的质量mB=4kg,质量为mC=2kg的木块C置于木板B上,水平面光滑,B、C之间有摩擦,现使A以vo=10m/s的初速度向右运动,与B碰撞后以立即以4m/s的速度弹回.求: