题目内容
【题目】如图所示,两个质量均为m的小球通过两根轻弹簧A、B连接,在水平外力F作用下,系统处于静止状态,此时弹簧实际长度相等。弹簧A、B的劲度系数分别为kA、kB,且原长相等。弹簧A、B与竖直方向的夹角分别为θ与45°。设A、B中的拉力分别为FA、FB。小球直径相比弹簧长度可以忽略。则( )
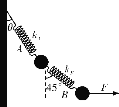
A. kA=kBB. tan θ=![]()
C. FA=![]() mgD. FB=2mg
mgD. FB=2mg
【答案】B
【解析】
将两小球看作一个整体,对整体受力分析,可知整体受到重力2mg,弹簧A的拉力FA和F的作用,受力如图甲所示,根据共点力的平衡条件有:![]() ,F=2mgtan θ,根据胡克定律:FA=kAxA,FB=kBxB,对下边的小球进行受力分析,其受力如图乙所示:
,F=2mgtan θ,根据胡克定律:FA=kAxA,FB=kBxB,对下边的小球进行受力分析,其受力如图乙所示:
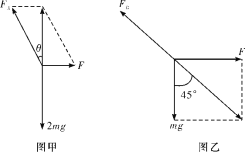
根据平衡条件有:FB=![]() mg,F=mg,联立可得:tanθ=
mg,F=mg,联立可得:tanθ=![]() ,故B正确,D错误;由tanθ=
,故B正确,D错误;由tanθ=![]() 知,cosθ=
知,cosθ=![]() ,得FA=
,得FA=![]() mg,故C错误;两个弹簧的原长相等,伸长后的长度也相等,所以弹簧的形变量也相等,而两个弹簧的弹力不同,所以两个弹簧的劲度系数不相等,故A错误。所以B正确,ACD错误。
mg,故C错误;两个弹簧的原长相等,伸长后的长度也相等,所以弹簧的形变量也相等,而两个弹簧的弹力不同,所以两个弹簧的劲度系数不相等,故A错误。所以B正确,ACD错误。

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目