题目内容
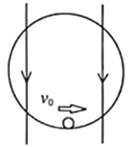
【题目】如图所示，导体框位于竖直平面内，匀强磁场垂直于纸面向里，磁感应强度大小B=2.0T，水平导体棒MN可沿两侧足够长的光滑导轨下滑而不分离，导体棒MN质量m=0.1kg，接入电路的电阻r=1.0Ω；导轨宽度L=1.0m，定值电阻R=3.0Ω，装置的其余部分电阻可忽略不计。将导体棒MN无初速度释放，导体棒下滑h=2.0m高度时速度达到最大，重力加速度g=10m/s2。则导体棒
A. 下滑的最大速度为4m/s
B. 从释放到下滑h高度所经历时间为2.1s
C. 从释放到下滑h高度过程中，电阻R产生的热量为1.95J
D. 从释放到下滑h高度过程中，通过电阻R的电荷量为1C
【答案】BD
【解析】
分析可知，导体棒无初速度释放，导体棒做加速度逐渐较小的加速度运动，当重力和安培力相等时，加速度为零，速度最大。全电路电阻上产生的焦耳热
，数值上等于克服安培力做的功，根据串联电路中热量与电阻的分配关系，可得
；根据感应电流的平均值，可推导出电荷量公式
，可计算通过电阻R的电荷量。
A、导体棒速度最大时，安培力等于重力，即：
，其中
，联立得：
，
，代入数据得：
，A错误；
C、由动能定理可知：
，解得：
，所以全电路电阻上的焦耳热
，所以电阻R上消耗的热量
，C错误
D、导体下落h的过程中，通过导线横截面的电量
，D正确。
B、导体棒下落h=2m的过程中，设经历时间为t，根据动量定理得：
，即
，代入数据解得：
，B正确。
故选BD。
练习册系列答案
相关题目
