题目内容
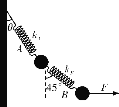
【题目】有一内壁光滑的圆管竖直放置,圆管底部封闭,上端开口且足够长,圆管内有两个小球A与B, A的质量为m1=0.1kg, B的质量为m2=0.2kg,两小球直径略小于管的直径。某时刻当B球向下运动至离圆管底面高度h=1m处时与向上运动的A球发生弹性碰撞,碰后B球向上运动至最大高度又返回到原来高度h=1m处,再次与已经和底面做完弹性碰撞后反弹 回来的小球A相碰,如此反复,做周期性运动,问要完成这种反复运动小球A与B碰前的速度应是多少? ( g取10m/s2)
![]()
【答案】4m/s,2m/s
【解析】
小球A和B各自碰前与碰后的速率应相等,对于碰撞过程,运用动量守恒定律得到质量与速度关系.对A、B两球运用运动学位移公式分析运动时间与速度的关系,联立求解即可.
设碰时A球与B球的速率分别为v1与v2,为完成反复运动,小球A和B各自碰前与碰后的速率应相等,即小球A碰后速度为-v1,小球B碰后速度为-v2,
则有![]()
得![]()
设小球A到达底面所需时间为t ,则有![]()
小球A往返一次所需时间![]()
小球B往返一次需时![]()
按题意要求有t1= t2
即![]()
解得:v1=4m/s,v2=2m/s

练习册系列答案
相关题目