题目内容
【题目】如图所示,质量m=4kg的物体静止在水平面上,在外力F=25N作用下开始运动.已知F与水平方向的夹角为37°,物体的位移为5m时,具有50J的动能.求:

(1)此过程中,外力F所做的功;
(2)此过程中,物体克服摩擦力所做的功;
(3)物体与水平面间的动摩擦因素.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】试题分析:由于摩擦力不知道,所以从功的定义式无法求解,我们可以运用动能定理求解摩擦力做功;
对物体进行受力分析,把拉力正交分解,用μ表示摩擦力,可以根据功的定义式求出摩擦力。
解:(1) ![]() ;
;
(2) 运用动能定理:
![]()
代入数据可得: ![]() ;
;
(3) 对物体进行受力分析:
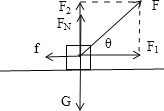
把拉力在水平方向和竖直方向分解,根据竖直方向平衡和滑动摩擦力公式得出:
f=μFN=μ(mg-Fsinθ)
根据功的定义式:Wf=μ(mg-Fsinθ)s
代入数据解得:μ=0.4。
点晴:动能定理的应用范围很广,可以求速度、力、功等物理量,特别是可以去求变力功,对于一个量的求解可能有多种途径,我们要选择适合条件的并且简便的。

【题目】(8分)如图下图所示是某同学探究加速度与力的关系的实验装置.他在气垫导轨上安装了一个光电门B,滑块上固定一遮光条,滑块用细线绕过气垫导轨左端的定滑轮与力传感器相连,传感器下方悬挂钩码,每次滑块都从A处由静止释放.


①该同学用游标卡尺测量遮光条的宽度d,如上图所示,则d=________mm.
②实验时,将滑块从A位置由静止释放,由数字计时器读出遮光条通过光电门B的时间t,若要得到滑块的加速度,还需要测量的物理量是________;
③下列必要的实验要求是________.(请填写选项前对应的字母)
A.应使滑块质量远大于钩码和力传感器的总质量 |
B.应使A位置与光电门间的距离适当大些 |
C.应将气垫导轨调节水平 |
D.应使细线与气垫导轨平行 |
④改变钩码质量,测出对应的力传感器的示数F和遮光条通过光电门的时间t,通过描点作出线性图象,研究滑块的加速度与力的关系,处理数据时应作出________图象.(选填“![]() ”、“
”、“![]() ”或“
”或“![]() ”).
”).







