题目内容
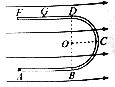
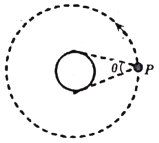
【题目】如图所示,飞行器P绕某星球做匀速圆周运动。测得该星球对飞行器的最大张角为θ,飞行器离星球表面的高度为h,绕行周期为T.已知引力常量为G,由此可以求得
A. 该星球的半径
B. 该星球的平均密度
C. 该星球的第一宇宙速度
D. 该星球对飞行器的引力大小
【答案】ABC
【解析】
A.由题意,令星球的半径为R,则飞行器的轨道半径r=R+h,由几何关系![]() ,即
,即![]() ,表达式中只有一个未知量R,故可以据此求出星球半径R;故A正确.
,表达式中只有一个未知量R,故可以据此求出星球半径R;故A正确.
B.由A项分析知,可以求出飞行器轨道半径r,据万有引力提供圆周运动向心力![]() 可知,已知r和T及G的情况下可以求得星球质量M,再根据密度公式
可知,已知r和T及G的情况下可以求得星球质量M,再根据密度公式![]() 可以求得星球的密度,故B正确.
可以求得星球的密度,故B正确.
C.在求得星球质量M及星球轨道半径R的情况下,根据![]() ,已知引力常量G,可以求出星球的第一宇宙速度,故C正确;
,已知引力常量G,可以求出星球的第一宇宙速度,故C正确;
D.因为不知道飞行器的质量大小,故无法求得星球对飞行器的引力大小,故D错误.

练习册系列答案
相关题目