题目内容
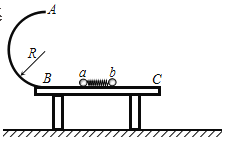
【题目】如图所示,半径为R的光滑半圆轨道AB竖直固定在一水平光滑的桌面上,轨道最低点B与桌面相切并平滑连接,桌面距水平地面的高度也为R。在桌面上轻质弹簧被a、b两个小球挤压(小球与弹簧不拴接),处于静止状态。已知a球的质量为m0,a、b两球质量比为2∶3。固定小球b,释放小球a,a球与弹簧分离后经过B点滑上半圆环轨道并恰能通过轨道最高点A。现保持弹簧形变量不变同时释放a、b两球,重力加速度取g,求:a球在半圆轨道上上升的最大高度H。
【答案】![]()
【解析】
设a、b两球的质量为ma、mb,由已知得ma=m0,mb=1.5m0。a球在B点时的速度为vB,恰能通过半圆环轨道最高点A时的速度为vA,则有
![]()
![]()
①轻弹簧具有的弹性势能释放时全部转化成小球a的机械能,a球从释放到运动至A点过程中机械能守恒,则有
Ep=![]() ②
②
以a、b、弹簧为研究对象,弹开时系统动量守恒、能量守恒,a、b的速度分别为va、vb,则有
![]() ③
③
![]() ④
④
又
![]() ⑤
⑤
由③④⑤解得
![]()
设a球上升至最大高度时速度为0,则有
![]()
解得![]() >R,可见a球会在某处脱离半圆轨道,设脱离时a球速度为v,脱离位置半径与竖直方向的夹角为α,根据圆周运动向心力公式有
>R,可见a球会在某处脱离半圆轨道,设脱离时a球速度为v,脱离位置半径与竖直方向的夹角为α,根据圆周运动向心力公式有
![]() ⑧
⑧
根据几何关系有
![]() ⑨
⑨
根据机械能守恒有
![]() ⑩
⑩
解得![]() 。
。
答:![]() 。
。

练习册系列答案
相关题目