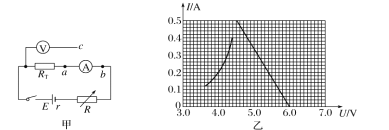
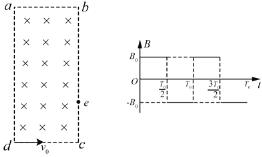
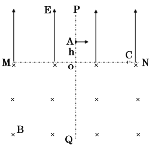
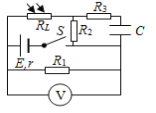
题目内容
【题目】如图所示，一质量为M=4kg的长木板B静止在光滑的水平面上，在长木板B的最右端放置一可视为质点的小铁块A，已知长木板的长度为L=1.4m，小铁块的质量为m=1kg，小铁块与长木板上表面之间的动摩擦因数为μ=0.4，重力加速度g=10m/s2。如果在长木板的右端施加一水平向右的恒力F=28N，求：
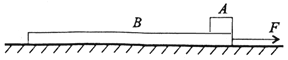
(1)小铁块与木板的加速度大小；
(2)为了保证小铁块能离开长木板，恒力F的作用时间至少应为多大？
【答案】(1)小铁块的加速度为：
长木板的加速度为：
(2)设恒力F作用时间至少为1s.
【解析】
根据在长木板的右端施加一水平向右的恒力F=28N可知，由牛顿第二定律求解B的加速度大小，根据能量关系列方程，整体整个过程中根据动量定理列方程求解即可。
(1) 根据牛顿第二定律得：
小铁块的加速度为：
长木板的加速度为：
；
(2) 设恒力F作用时间为t，小铁块在长木板上滑动距离为L1，
由空间关系可知
整理得：
此时，小铁块的速度
长木板的速度
撤去F后，小铁块和长木板组成的系统动量守恒，则由动量守恒定律得：
解得：
若滑块刚好滑到木板的最左端，由能量守恒得：
代入数据解得：
。
练习册系列答案
相关题目
