题目内容
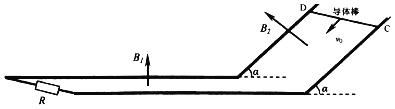
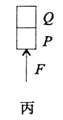
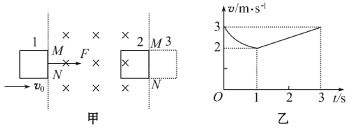
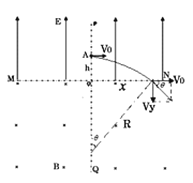
【题目】如图所示,在不考虑万有引力的空间里,有两条相互垂直的分界线MN、PQ,其交点为O。MN一侧有电场强度为E的匀强电场(垂直于MN),另一侧有匀强磁场(垂直纸面向里)。宇航员(视为质点)固定在PQ线上距O点为h的A点处,身边有多个质量均为m、电量不等的带负电小球。他先后以相同速度v0、沿平行于MN方向抛出各小球。其中第1个小球恰能通过MN上的C点第一次进入磁场,通过O点第一次离开磁场,OC=2h。求:
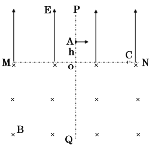
(1)第1个小球的带电量大小;
(2)磁场的磁感强度的大小B;
(3)磁场的磁感强度是否有某值,使后面抛出的每个小球从不同位置进入磁场后都能回到宇航员的手中?如有,则磁感强度应调为多大。
【答案】(1) ![]() ;(2)
;(2) ![]() ;(3)存在,
;(3)存在,![]()
【解析】
(1)设第1球的电量为![]() ,研究A到C的运动:
,研究A到C的运动:
![]()
![]()
解得:![]() ;
;
(2)研究第1球从A到C的运动:
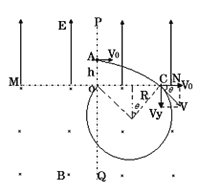
![]()
解得:![]()
![]() ,
,![]() ,
,![]() ;
;
研究第1球从C作圆周运动到达O的运动,设磁感应强度为![]()
由![]() 得
得![]()
由几何关系得:![]()
解得:![]() ;
;
(3)后面抛出的小球电量为![]() ,磁感应强度
,磁感应强度![]()
①小球作平抛运动过程
![]()
![]()
②小球穿过磁场一次能够自行回到A,满足要求:![]() ,变形得:
,变形得:![]()
解得:![]() 。
。

练习册系列答案
相关题目