题目内容
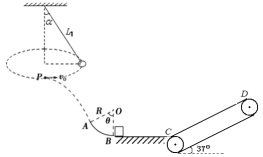
【题目】如图所示，长为L1=2m的细线拴一质量为m=1kg的小球在水平面内做匀速圆周运动(圆锥摆),摆线与竖直方向的夹角为α=37°,不计空气阻力，当小球运动到P点时绳子断了，一段时间后小球恰好从光滑圆弧ABC的A点沿切线方向进入圆弧，进入圆弧时无机械能损失，已知圆弧的半径R=
m，θ=53°，小球经圆弧运动到B点时与停在光滑地面的质量为M=2 kg的物块发生弹性正碰，物块运动到C后沿顺时针转动的倾斜的传送带CD运动，传送带CD与地面的倾角
=37°，速度为v=2m/s，不计物块在C处的机械能损失。已知物块与传送带间的动摩擦因数为0.5（g取10 m/s2，sin37°=0.60，cos 37°=0.80，g取 10 m/s2)求：
（1）小球到达圆弧B点时（碰撞前）的速度
（2）若物块M若能够到达D端，传送带CD部分L2最长是多少
【答案】（1）
（2）
【解析】
（1）设匀速圆周运动速度
：
，解得：
，在A点，设速度为
，根据运动合成与分解：
，从A到B，设碰前速度
，根据动能定理：
，解得：
（2）两物体弹性相碰，设M碰后速度为
，m碰后速度为
：
，
，解得：
，开始滑上传送带，在传送带上，开始减速，到与传送带速度相同：
，
，因为
，所以共速后，不能一起匀速，继续减速
，减速到零：
，所以传送带最长
练习册系列答案
心算口算巧算一课一练系列答案
应用题作业本系列答案
相关题目
