Question

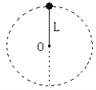
【题目】如图所示，半径为R的竖直光滑圆轨道内侧底部静止着一个光滑小球，现给小球一个冲击使它在瞬间得到一个水平初速度v0，v0大小不同则小球能够上升到的最大高度（距离底部）H也不同。下列说法中正确的是

A．时，

B．时，

C．时，

D．时，

Answer 1

【答案】AD

【解析】

试题分析：当v0=时，根据机械能守恒定律有：mv02=mgh，解得h=R，即小球上升到高度为R

时速度为零，所以小球能够上升的最大高度为R，故A正确；设小球恰好运动到圆轨道最高点时，在最低点的速度为v1，在最高点的速度为v2，则在最高点，有，从最低点到最高点的过程中，根据机械能守恒定律得：2mgR+mv22=mv12解得 v1=所以v0＜时，在小球不能上升到圆轨道的最高点，会脱离轨道最高点的速度不为零，根据mv02=mgh+mv′2，知最大高度 h＜R，故B错误；

由上分析知，当v0=时，上升的最大高度为2R，设小球恰好能运动到与圆心等高处时在最低点的速度为v，则根据机械能守恒定律得：mgR=mv2，解得v=，因为＜＜，在小球不能上升到圆轨道的最高点，会脱离轨道，则小球能够上升的最大高度小于2R，故C错误，D正确．故选AD．