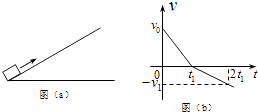��Ŀ����
����Ŀ����ͼ��a��������L=0.8m�Ĺ⻬����˹̶�һ������ĵ���A��������Q=1.8��10��7C��һ����m=0.02kg��������Ϊq��С��B���ڸ��ϣ�������ˮƽ����̶���ij�Ǿ�����糡�У��Ը����Ϊԭ�㣬�ظ�����Ϊx��������������ϵ������A��С��B����������Bλ��x�ı仯��ϵ��ͼ��b��������I��ʾ��С��B����ˮƽ����ĺ�����Bλ��x�ı仯��ϵ��ͼ��b��������II��ʾ����������II��0.16��x��0.20��x��0.40��Χ�ɽ��ƿ���ֱ�ߣ�������������k=9��109Nm/C2��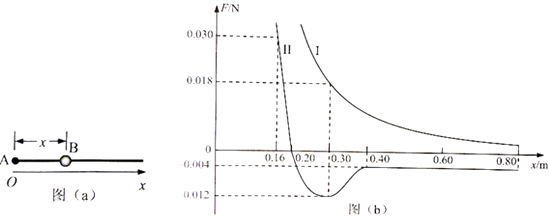
��1����B��������q��
��2���Ǿ�����糡��x=0.3m����ϸ�˷���ĵ糡ǿ�ȴ�СE��
��3���ںϵ糡�У�x=0.4m��x=0.6m֮��ĵ��Ʋ�U��
��4����֪С����x=0.2m�����v=0.4m/s�ij��ٶ�ʱ����Զ�����˶���x=0.4m����С����x=0.16m�����ܵ��������ң���СΪ0.04N�ĺ������ú��ɾ�ֹ��ʼ�˶���ΪʹС�����뿪ϸ�ˣ��������õ���С����s�Ƕ��٣�
���𰸡�
��1��
�⣺��ͼ��֪����x=0.3mʱ�� ![]() N
N
��� q= ![]() =
= ![]() C=1��10��6C
C=1��10��6C
��2��
�⣺����x=0.3m��������С���������ΪF2���� F��=F2+qE
��� ![]()
���糡��x=0.3m����ϸ�ѷ���ĵ糡ǿ�ȴ�СΪ3��104N/C����������
��3��
�⣺����ͼ���֪��x=0.4m��x=0.6m֮��������� W=��8��10��4J
��qU=W���ɵ� U=��800V
��4��
�⣺��ͼ��֪С���x=0.16��x=0.2m����
�糡������ ![]()
���x=0.2m��x=0.4m�� W2=�� ![]() mv2=��
mv2=�� ![]() ��0.02��0.42=��1.6��10��3 J
��0.02��0.42=��1.6��10��3 J
��ͼ��֪С���x=0.4m��x=0.8m��
�糡������ W3=��0.004��0.4=��1.6��10��3
�ɶ��ܶ�����
W1+W2+W3+F��s=0
��� s=�� ![]()
�������ݽ�� s=0.065m
����������1����ͼ����x=0.3mʱ�Ŀ����������ݿ��ض��ɿ���С��B������������2�����ݵ糡ǿ�ȵĶ������Ǿ�����糡��x=0.3m����ϸ�˷���ĵ糡ǿ�ȴ�С����3���ںϵ糡�У����ݵ糡��������x=0.4m��x=0.6m֮��ĵ��Ʋ��4���ֱ�������ε糡�����Ĺ������ɶ��ܶ�����������õ���С���룮

 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�