题目内容
【题目】如图所示，水池正上方p点处有一小球，球距水面h1=3.2m，池水深h2=1.6m，小球由p点开始做自由落体运动，落入水中后做匀减速直线运动，到池底的速度恰好为零，（取g=10m/s2）求：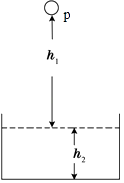
（1）小球运动的最大速度；
（2）从开始到落到池底所用的时间．
【答案】
（1）解：小球下落到水面时速度最大，有：
代入数据： 
答：小球运动的最大速度为8m/s；
（2）解：小球下落到水面的时间为 
，有：
解得： 
在水池中减速运动的加速度大小为a，由速度位移关系有：
代入数据： 
减速运动的时间为 
解得： 
运动时间： 
=1.2s
答：从开始到落到池底所用的时间为1.2s
【解析】整个过程是先从静止做自由落体运动，在接触水面的那一刻达到最大速度，然后做匀减速直线运动，在到达池底速度减为0，将整个运动过程划分为两个 阶段分别应用运动学公式即可求解。
【考点精析】认真审题，首先需要了解自由落体运动(（1）条件:初速度为零，只受重力作用；（2）性质:是一种初速为零的匀加速直线运动，a=g)，还要掌握匀变速直线运动的速度、位移、时间的关系(速度公式：V=V0+at；位移公式：s=v0t+1/2at2；速度位移公式：vt2-v02=2as；以上各式均为矢量式，应用时应规定正方向，然后把矢量化为代数量求解，通常选初速度方向为正方向，凡是跟正方向一致的取“+”值，跟正方向相反的取“-”值)的相关知识才是答题的关键．
练习册系列答案
相关题目
