题目内容
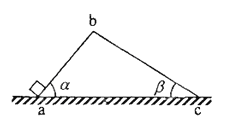
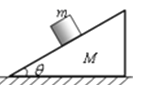
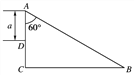
【题目】如图所示，高为h、粗糙程度不同的倾斜轨道AB、CD与水平面的夹角均为45°，它们分别与竖直平面内的圆弧形光滑轨道相切于B、C两点。质量为m的小滑块从A点由静止滑下后，经CD轨道返回，再次冲上AB轨道至速度为零时，相对于BC面的高度为
．已知小滑块与AB轨道间的动摩擦因数为0.5，重力加速度为g，求：
（1）小滑块第一次到达C点时的速度大小；
（2）小滑块沿CD面向上滑动的最大距离。
【答案】（1）
（2）
【解析】
(1)由A→C由动能定理得：mgh-（μ1mgcos45°）
=
mvC2
解得：
vC=
(2)从C到CD斜面的最高点由动能定理得：-（mgsin45°+μ2mgcos45°）x=0-mvC2
从CD斜面最高点到停止位置由动能定理得：
（mgsin45°-μ2mgcos45°）x-（mgsin45°+μ1mgcos45°）
=0
解得：
x=
练习册系列答案
相关题目
