Question

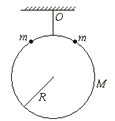
【题目】如图所示，A、B是地球的两颗卫星，卫星A、B的圆形轨道位于赤道平面内，运行方向与地球自转方向相同。卫星A离地面高度为7R，卫星B离地面高度为R，R为地球半径，地球表面的重力加速度为g，O为地球中心。

（1）求卫星A、B的运行周期之比。

（2）若某时刻A、B两卫星相距最近（O、B、A在同一直线上），则至少经过多长时间，它们再一次相距最近？

Answer 1

【答案】（1）8：1（2）

【解析】

由万有引力提供向心力：G=m=mω2r=m（）2r 解得：

T==2πω=

(1)由T==2π可知：

===8

(2)由ω=又gR2=GM则得:

ω=

则有：

ωA=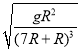

ωB=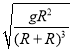

得它们再一次相距最近时，一定是B比A多转了一圈，有：（ωB-ωA）t=2π

由以上各式可得：

t=