题目内容

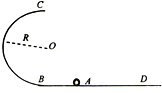
如图所示，一光滑半圆形轨道ABC固定在竖直面内，半径R=2.5m，轨道底端与水平地面相切于C点，一小球从C点以某一水平向左的速度冲上半圆轨道，到达最高点A时对轨道压力刚好为0，离开A后落在水平地面上的D点，取g=10m/s2．求：
（1）小球通过A点时的速度；
（2）C、D间的距离SCD．
（1）小球在最高点A时对轨道压力刚好为0，即重力恰好提供向心力，则有：mg=
vA2
R

解得：vA=
gR
=
25
=5m/s
（2）从A点抛出后做平抛运动，则
t=
2h
g
=
4R
g
=1s
水平方向有：SCD=vAt=5×1=5m
答：（1）小球通过A点时的速度为5m/s；
（2）C、D间的距离SCD为5m．
练习册系列答案
相关题目
如图所示，过山车的轨道可视为竖直平面内半径为R的圆轨道，为了安全要求过山车必须以较大的速度通过最高点．质量为m的游客随过山车一起运动，当过山车以速度v经过圆轨道的最高点时（　　）
A．座椅对人的作用力大于mg
B．向心加速度方向竖直向下
C．速度v的大小大于
gR
D．座位对游客的作用力为m
v2
R
如图所示，光滑水平面上，质量为m的小球在拉力F作用下做匀速圆周运动．若小球运动到P点时，拉力F发生变化，下列关于小球运动情况的说法中正确的是（　　）
A．若拉力突然消失，小球将沿轨迹Pa做离心运动
B．若拉力突然变小，小球将沿轨迹Pb做离心运动
C．若拉力突然变大，小球将沿轨迹Pb做离心运动
D．若拉力突然变小，小球将沿轨迹Pc做向心运动
杂技演员在表演水流星节目时，在最高点杯口向下时水也不会流出来，这是因为（　　）
A．水受到离心作用
B．水处于失重状态，不受重力作用
C．重力和水杯底的压力的合力作为向心力的作用，起到使水改变运动方向的作用
D．水受到重力、杯底压力和向心力的作用，合力为零
如图所示，物块在水平圆盘上与圆盘一起绕固定轴匀速转动，说法不正确的是（　　）
A．物块运动的角速度不变
B．物块受三个力作用，由静摩擦力提供向心力
C．在角速度一定时，物块到转轴的距离越远，越不容易脱离圆盘
D．物块到转轴距离一定时，物块运动周期越小，越容易脱离圆盘
一辆汽车总质量为2.0×103Kg，这辆汽车以10m/s的速率通过凸圆弧形桥，桥的圆弧半径为50m，则汽车通过桥顶部时，桥面受到汽车的压力大小为______N，如果这辆汽车通过凸形桥顶部时速度达到______m/s，汽车就对桥面无压力．
如图，在竖直平面内有一固定光滑轨道，BD是水平直轨道，BC是圆心为O、半径为R的
1
2
圆弧轨道，两轨道相切于B点．在外力作用下，一小球从A点由静止开始做匀加速直线运动，到达B点时撤除外力，AB两点的距离为R，已知小球刚好能沿圆轨道经过最高点C，重力加速度大小为g．求：
（1）小球在最高点C的速度大小；
（2）AB段运动的加速度的大小；
（3）小球从C点抛出落到D点时运动的水平距离．
如图所示，半径为L的圆管轨道（圆管内径远小于轨道半径）竖直放置，管内壁光滑，管内有一个小球（小球直径略小于管内径）可沿管转动，设小球经过最高点P时的速度为v，则（　　）
A．v的最小值为
gL
B．v若增大，球所需的向心力也增大
C．当v由
gL
逐渐减小时，轨道对球的弹力也减小
D．当v由
gL
逐渐增大时，轨道对球的弹力也增大
如图所示，轻绳的一端固定在O点，另一端系一质量为m的小球（可视为质点）．当小球在竖直平面内沿逆时针方向做圆周运动时，通过传感器测得轻绳拉力T、轻绳与竖直线OP的夹角θ满足关系式T=a+bcosθ，式中a、b为常数．若不计空气阻力，则当地的重力加速度为（　　）
A．
b
2m
B．
2b
m
C．
3b
m
D．
b
3m

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网