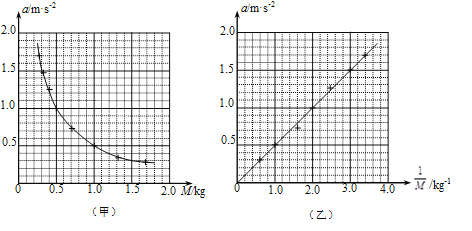
��Ŀ����
����Ŀ�����˶Ա�����ըҩ��ը������������Ũ�����Ȥ�����������ʵ�飬��һ�⻬ˮƽ���Ϸ�����������Ϊ�ʵ�Ľ����ŵ�A��B�������壬���ǵ������ֱ�Ϊm1=1kg��m2=3kg����������֮�������ըҩ��ˮƽ������һ���Եĵ��壬ˮƽ���ҷ���һ�⻬�� ![]() ��ֱԲ���������A��B���ᄇֹ����ȼըҩ���䱬ը������A�����˶��뵲������ԭ�ٷ��أ���ˮƽ����������B��������ײ��ճ��һ�����ǡ�ܵ���Բ����ߵ㣬��֪Բ���İ뾶ΪR=0.2m��g=10m/s2 �� ��ըҩ��ըʱ��A��B�����������Ĺ���
��ֱԲ���������A��B���ᄇֹ����ȼըҩ���䱬ը������A�����˶��뵲������ԭ�ٷ��أ���ˮƽ����������B��������ײ��ճ��һ�����ǡ�ܵ���Բ����ߵ㣬��֪Բ���İ뾶ΪR=0.2m��g=10m/s2 �� ��ըҩ��ըʱ��A��B�����������Ĺ���
���𰸡��⣺ըҩ��ը����A���ٶȴ�СΪv1��B���ٶȴ�СΪv2��ȡ����Ϊ�������ɶ����غ㶨�ɵ�
m1v1��m2v2=0
A���뵲��������B��������ﹲͬ�ٶ���Ϊv��ȡ����Ϊ�������ɶ����غ㶨�ɵ�
m1v1+m2v2=��m1+m2��v
��������ƤԲ������ߵ�ʱ�ٶ�Ϊ0��������Ķ���ת��Ϊ�������ܣ��ɻ�е���غ㶨�ɵ�
![]() ��m1+m2��v2=��m1+m2��gR
��m1+m2��v2=��m1+m2��gR
ըҩ��ըʱ��A��B�����������Ĺ� W= ![]() m1v12+
m1v12+ ![]() m2v22��
m2v22��
������� W=10.7J
��ըҩ��ըʱ��A��B�����������Ĺ�Ϊ10.7J��
��������A���뵲��������B��Ĺ����ж����غ㶨�ɣ���������ƤԲ������ߵ�Ĺ����л�е���غ㶨�ɣ��ⷽ������⼴�ɡ�
�����㾫�����������⣬������Ҫ�˽��е���غ㼰������(��ֻ���������͵��ɵ����������������£����嶯�ܺ��������ܣ����������ܣ������ת��������е�ܵ��������ֲ���)����Ҫ���ն����غ㶨��(�����غ㶨�ɳ�����������ϵͳ����������ϵͳ���������ĺ���Ϊ�㣻ϵͳ���ܵ������ĺ����䲻Ϊ�㣬��ϵͳ����������С�öࣻϵͳ���������ĺ����䲻Ϊ�㣬����ij�������ϵķ���Ϊ�㣬���ڸ÷�����ϵͳ���ܶ����ķ������ֲ���)�����֪ʶ���Ǵ���Ĺؼ���

 �¿α�������������ҵ�������γ�����ϵ�д�
�¿α�������������ҵ�������γ�����ϵ�д�