题目内容
【题目】如图所示，小球从光滑的半径为R的半圆槽顶部A由静止滑下，小球的质量为m，半圆槽的质量为M=3m，半圆槽与桌面无摩擦，小球的大小忽略不计，求：
（1）当小球运动到半圆槽底部时的小球速度；
（2）当小球下落 
R时半圆槽的速度．
【答案】
（1）解：小球与半圆槽组成的系统在水平方向上动量守恒，取水平向右为正方向，由水平方向动量守恒得：
Mv1﹣mv2=0
由于没有摩擦，所以系统的机械能守恒，则得：
mgR= 
Mv12+ mv22．
解得，当小球运动到半圆槽底部时的小球速度为：
v2= 
答：当小球运动到半圆槽底部时的小球速度是 ；
（2）设小球下落 
R时的速度为v2′，半圆槽的速度为v1′，如图所示，小球与半圆槽组成的系统在水平方向上动量守恒，得：
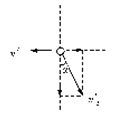
Mv1′﹣mv2′sinα=0
小球相对半圆槽的速度方向与水平方向成45°，有：
v1′+v2′sinα=v2′cosα
根据机械能守恒得： mgR= Mv1′2+ mv2′2．
解得：v1′= 
答：当小球下落 R时半圆槽的速度是 ．
【解析】（1）以小球与半圆槽组成的系统为研究对象，根据动量守恒条件和机械能守恒定律列式子求解即可。
（2）以小球与半圆槽组成的系统为研究对象，运用速度的分解结合动量动量守恒和机械能守恒定律列式子联立求解。
【考点精析】通过灵活运用动量守恒定律和能量守恒定律，掌握动量守恒定律成立的条件：系统不受外力或系统所受外力的合力为零；系统所受的外力的合力虽不为零，但系统外力比内力小得多；系统所受外力的合力虽不为零，但在某个方向上的分量为零，则在该方向上系统的总动量的分量保持不变；能量守恒定律：能量既不会消灭，也不会创生，它只会从一种形式转化为其他形式，或者从一个物体转移到另一个物体，而在转化和转移过程中，能量的总量保持不变即可以解答此题．
