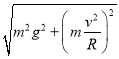题目内容
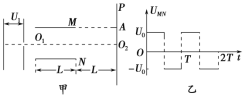
【题目】如图所示,位于平面直角坐标系内的水平正对的平行金属板的长度为L,板间距离也为L,金属板之间存在匀强电场,金属板厚度忽略不计，第一象限内边长也为L的正方形区域ABCD为无场区。在平行金属板和正方形区域的外侧存在范围足够大的匀强磁场,磁场的方向垂直XY平面向里。一个质量为m、电荷量为q的带正电的粒子沿两平行金属板的中线OO'射入电场,初速度为v,粒子恰好从下极板的右端A点离开电场。已知带电粒子进入磁场后能通过B点(粒子只在AB下方偏转),不计粒子重力。
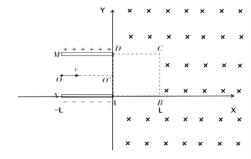
（1）求粒子第一次进入磁场时速度的大小和方向；
（2）求匀强磁场的磁感应强度大小；
（3）若仅将匀强磁场的磁感强度变为原来的两倍,求粒子从离开电场到回到电场所用的时间。
【答案】（1）
，在A点的速度方向与水平方向的夹角
（2）2mv/qL（3）
【解析】
带电粒子在偏转电场中做类平抛运动，根据水平和竖直方向的运动规律求解出离电场的速度和方向；根据圆周运动的规律结合几何知识求解匀强磁场的磁感应强度大小；将磁感应强度变为原来的两倍，带电粒子做圆周运动的轨道半径变为原来的一半。画出粒子在磁场区域及在ABCD区域的轨迹图；根据轨迹求解时间.
（1）带电粒子在电场中做类平抛运动，有L=vt
L=at2
根据类平抛运动的知识有：vy=at；
tanα=vy/v=1
可得粒子在A点的速度方向与水平方向的夹向α=45° 解得：v'=v/cosα=
v
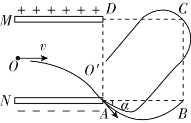
（2）画出粒子从A到B做圆周运动的运动轨迹，如图所示；
根据几何知识得：L=2Rsinα
解得L=R
再根据qv'B=mv'2/R；
解得B=
（2）将磁感应强度变为原来的两倍，带电粒子做圆周运动的轨道半径变为原来的一半。画出粒子在磁场区域及在ABCD区域的轨迹图；根据粒子的运动轨迹，可知粒子在磁场中运动了3/4个周期，其中周期T'=T/2，时间为
；粒子在ABCD区域内部运动的时间为t2=
总时间t=t1+t2=
