��Ŀ����
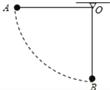
����Ŀ����ͼ��ʾ�����Ϊ37��Ĵֲ�б��AB����뾶R=0.4m�Ĺ⻬��Բ���BCƽ��������OΪ���Բ�ģ�BCΪԲ���ֱ���Ҵ�����ֱ����A��C����ȸߡ�����m=1kg�Ļ����A���ɾ�ֹ��ʼ�»���ǡ�ܻ�����O�ȸߵ�D�㣬��gȡ10m/s2��sin37=0.6�� cos37=0.8��

��1������б���Ķ�Ħ�������̡�
��2����ʹ�����ܵ���C�㣬���A����б�滬��ʱ�ij��ٶ�v0����Сֵ��
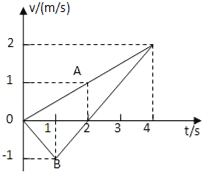
��3���������뿪A�����ٶȴ�СΪ![]() m/s�����C��ɳ����䵽б���ϵ�ʱ��t��
m/s�����C��ɳ����䵽б���ϵ�ʱ��t��
���𰸡���1��0.375 ��2��![]() ��3��0.2s
��3��0.2s
��������
�����������1���Դ�A��B��Dȫ�����о���֧�����Ի��鲻������������������Ħ���������������ݶ��ܶ����ã�
![]()
�ɼ���֪ʶ֪��![]()
������ʽ������ã�������б���Ķ�Ħ������Ϊ![]()
��2���������ܵ���C�㣬����C��Ӧ��������С��ĵ���![]()
����ţ�ٵڶ����ɵã�
![]()
������ã�![]()
A��B��D��C���̣�����A��C����ȸߣ�������������Ϊ�㣬֧����ʼ�����ٶȴ�ֱ���Ի��鲻���������ݶ��ܶ����ã�
![]()
�ɼ���֪ʶ֪��![]()
������ã�![]()
���Ի����A����б�滬��ʱ�ij��ٶ�v0����СֵΪ![]()
��3���������뿪A�����ٶȴ�СΪ![]() m/sʱ���軬�鵽��C����ٶȴ�СΪ
m/sʱ���軬�鵽��C����ٶȴ�СΪ![]() �����ݶ��ܶ����ã�
�����ݶ��ܶ����ã�
![]() ������ã�
������ã�![]()
�����뿪C�����ƽ���˶�������ƽ���˶����ɵã�
![]() ������
������![]()
�ɼ��ι�ϵ֪��![]()
��ʽ�����������������ã�![]()
��ã�![]()
���Ի����C��ɳ����䵽б���ϵ�ʱ��tΪ0.2s��

 ��������ϵ�д�
��������ϵ�д� ���ɶ���ܲ��¿�ֱͨ�߿�ϵ�д�
���ɶ���ܲ��¿�ֱͨ�߿�ϵ�д�