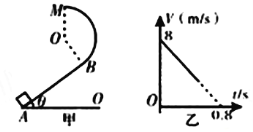题目内容
【题目】如图所示,足够长的光滑竖直平行金属轨道处于一个很大的匀强磁场中,已知轨道宽为l,磁感应强度大小为B、方向垂直轨道平面水平指向纸里。轨道上端接入一个滑动变阻器和一个定值电阻,已知滑动变阻器的最大阻值为R,定值电阻阻值为R/2。轨道下端有根金属棒CD恰好水平搁在轨道上,接触良好,已知金属棒质量为m。起初滑片P处于变阻器的中央,CD棒在一平行于轨道平面的竖直向上F作用下,以某一初速度开始向上做匀减速直线运动,已知初速度大小为v0,加速度大小为a。不考虑金属棒和轨道的电阻,重力加速度大小为g。则
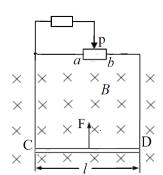
(1)请说明金属棒运动过程中棒中感应电流方向;
(2)保持滑片P位置不变,金属棒运动过程中经过多少时间时流过定值电阻的电流为零?此时外力F多大?
(3)保持滑片P位置不变,金属棒运动过程中经过多少时间时流过定值电阻的电流为I0(I0已知且非零值)?此时外力F多大?
【答案】(1)先C到D,后D到C;(2) ![]() ;F =mg-ma;(3)见解析;
;F =mg-ma;(3)见解析;
【解析】
(1)金属棒先向上匀减速直线运动,减到零后向下匀加速直线运动。因此根据右手定则,当金属棒CD向上运动时,棒中感应电流方向为:D→C;然后当金属棒CD向下运动时,棒中感应电流方向为: C→D ;
(2)若流过定值电阻的电流为零,则此时电路中没有感应电流,即感应电动势为零,根据E=BLv可知道,v=0。
根据运动学公式:0= v0+at,得到![]()
金属棒运动过程中经过流过定值电阻的电流为零,此时安培力为零,根据牛顿第二定律,得到mg-F=ma,此时外力F =mg-ma.
(3)当滑片处于中央时,并联电阻为R/4,回路总电阻为3R/4。流过定值电阻的电流为I0时,此时干路电流为2I0,
电动势为E=2I0![]() R=
R=![]() I0R ,根据E=BLv,得到
I0R ,根据E=BLv,得到![]()
讨论:金属棒先向上匀减速直线运动,后向下匀加速直线运动。
①当v0< ![]() 时,只在向下加速过程中,才出现流过定值电阻的电流为I0。根据运动学公式得到
时,只在向下加速过程中,才出现流过定值电阻的电流为I0。根据运动学公式得到![]() ,解得
,解得![]() ,经过时间
,经过时间![]() 流过定值电阻的电流为I0
流过定值电阻的电流为I0
此时根据牛顿第二定律得到:mg -F- FA=ma,
此时F =mg- ma- FA= mg- ma-2I0LB
②当v0=![]() ,在t1=0以及向下加速过程中,出现流过定值电阻的电流为I0。t2=
,在t1=0以及向下加速过程中,出现流过定值电阻的电流为I0。t2=![]() ;
;
t1=0时,棒向上运动,mg +FA-F =ma,得到此时F =mg+FA-ma = mg-ma+2I0LB
t2时,棒向下运动,mg -F- FA=ma,此时F =mg- ma- FA= mg- ma-2I0LB
③ 当v0> ![]() 时,向上和向下过程中都出现流过定值电阻的电流为I0
时,向上和向下过程中都出现流过定值电阻的电流为I0
向上过程中,由v=v0-at ,可得![]()
此时mg +FA-F =ma,得到此时F =mg+FA-ma = mg-ma+2I0LB
向下过程中,由-v=v0-at ,可得![]() ,
,
经过时间![]() ,此时mg -F- FA=ma,此时F =mg- ma- FA= mg- ma-2I0LB
,此时mg -F- FA=ma,此时F =mg- ma- FA= mg- ma-2I0LB