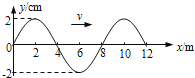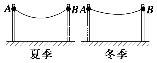��Ŀ����
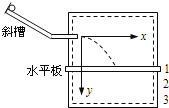
����Ŀ����ͼ��1����ʾ��һ���ᵯ���϶˹̶����¶�����һ������Ϊm��A�����ɵľ���ϵ��Ϊk��������ֱ������������A��ʹ����A��ֹ��ijһ��ʼλ�ã���ʱ���ɴ���ѹ��״̬����ͼ��2����ʾ���ָı��ֶ�����A����������ʹA��ijһ���ٶ�����ֱ���µ��ȼ���ֱ���˶�����֪����A�������ȼ���ֱ���˶�ʱ�����ٶȵ���ֵǡ�õ����ڳ�ʼλ��ʱͻȻ��ȥ�ֵ�˲ʱ����A���ٶ���ֵ��һ�룮��������A���˶������У�����ʼ��δ�����䵯���ȣ����ֶ�����A��������δ�ı䷽��ǰ������A�������ȼ���ֱ���˶�����������S����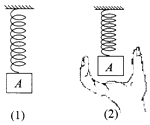
��1������A���ȼ���ֱ���˶��ļ��ٶ�a=��
��2��ͨ������S���õ�ʱ��t= ��
���𰸡�
��1��![]()
��2��![]()
���������⣺��ͻȻ��ȥ�ֵ�˲ʱ������A�����˶��ļ��ٶ�Ϊa����1�����ʼʱ�̵��ɵ�ѹ����Ϊx���о�������A����ţ�ٵڶ������У�
kx+mg=ma
�ã�x= ![]()
����֪����֪������A�������ȼ���ֱ���˶��ļ��ٶ� a��= ![]() �����ֶ�����A�������ķ����ı��˲ʱ���ֶ������������Ϊ�㣮
�����ֶ�����A�������ķ����ı��˲ʱ���ֶ������������Ϊ�㣮
��a���g�����ֶ�����A��������Ϊ��ʱ�����ɳ���δ����ԭ�������ʱ����ѹ����Ϊx�䣬�У�
kx��+mg=ma��
�ɵã�x��= ![]()
����A�����˶��ľ���Ϊ��
S=x��x��= ![]() =
= ![]()
����A�������ȼ���ֱ���˶��ļ��ٶ�Ϊ��
a��= ![]()
����S= ![]() ��������A�������ȼ���ֱ���˶�ʱ��Ϊ��
��������A�������ȼ���ֱ���˶�ʱ��Ϊ��
t= ![]() =
= ![]()
�� ![]() ��a�䣼g�����ֶ�����A��������Ϊ��ʱ�����ɳ����ѳ���ԭ�������ʱ�����쳤��Ϊx�壬�У�
��a�䣼g�����ֶ�����A��������Ϊ��ʱ�����ɳ����ѳ���ԭ�������ʱ�����쳤��Ϊx�壬�У�
mg��kx��=ma��
�ã�x��= ![]()
��S=x+x��= ![]() =
= ![]()
��ˣ���ʱ����A�������ȼ���ֱ���˶��ļ��ٶ�Ϊ��
a��= ![]()
ʱ����Ϊ��t= ![]() =
= ![]()
�ʴ�Ϊ����1�� ![]() ����2��
����2�� ![]() ��
��
ͻȻ��ȥ�ֵ�˲ʱ������ţ�ٵڶ�������ʽ����ͻȻ��ȥ�ֵ�˲ʱ������A�����˶��ļ��ٶ�Ϊa���������Ĺؼ�����ȷţ�ٵڶ����ɿ��о�ijһ״̬�ļ��ٶȣ�Ҫץס�����������ٽ�״̬�����ֶ�����A�������ķ����ı��˲ʱ��֪����ʱ�ֶ������������Ϊ�㣮Ҫ�ҳ�A�˶���λ���뵯���α����Ĺ�ϵ��

����Ŀ��������Ȼ���ң���������ֱʱ�����ȼ�ΪL�� �� �����¶˹���������ʱ�����ȼ�ΪL0������������ÿ������10g���룬���ɳ������μ�ΪL1��L6 �� �������±�����
|
��1��������һ����ֵ��¼���淶����������Ϊ �� �ɱ���֪���ÿ̶ȳߵ���С�ֶ�Ϊ ��
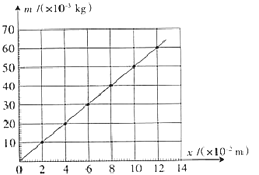
��2��ͼ�Ǹ�ͬѧ���ݱ�����������ͼ������������������������ǵ��ɳ������IJ�ֵ���L����L0������
��3����ͼ��֪���ɺ͵ľ���ϵ��ΪN/m��ͨ��ͼ�ͱ���֪�����̵�����Ϊg�����������λ��Ч���֣��������ٶ�ȡ9.8m/s2����