题目内容
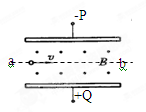
如图1所示,水平直线PQ下方有竖直向上的匀强电场,上方有垂直纸面方向的磁场,其磁感应强度B随时间的变化规律如图2所示(磁场的变化周期T=2.4×10-5s)。现有质量 带电量为
带电量为 的点电荷,在电场中的O点由静止释放,不计电荷的重力。粒子经t0=
的点电荷,在电场中的O点由静止释放,不计电荷的重力。粒子经t0= 第一次以
第一次以 的速度通过PQ,并进入上方的磁场中。取磁场垂直向外方向为正,并以粒子第一次通过PQ时为t=0时刻。(本题中取
的速度通过PQ,并进入上方的磁场中。取磁场垂直向外方向为正,并以粒子第一次通过PQ时为t=0时刻。(本题中取 ,重力加速度
,重力加速度 )。试求:
)。试求:
⑴ 电场强度E的大小;
⑵ 时刻电荷与O点的水平距离;
时刻电荷与O点的水平距离;
⑶ 如果在O点右方d=67.5cm处有一垂直于PQ的足够大的挡板,求电荷从开始运动到碰到挡板所需的时间。(保留三位有效数字)
 带电量为
带电量为 的点电荷,在电场中的O点由静止释放,不计电荷的重力。粒子经t0=
的点电荷,在电场中的O点由静止释放,不计电荷的重力。粒子经t0= 第一次以
第一次以 的速度通过PQ,并进入上方的磁场中。取磁场垂直向外方向为正,并以粒子第一次通过PQ时为t=0时刻。(本题中取
的速度通过PQ,并进入上方的磁场中。取磁场垂直向外方向为正,并以粒子第一次通过PQ时为t=0时刻。(本题中取 ,重力加速度
,重力加速度 )。试求:
)。试求:⑴ 电场强度E的大小;
⑵
 时刻电荷与O点的水平距离;
时刻电荷与O点的水平距离;⑶ 如果在O点右方d=67.5cm处有一垂直于PQ的足够大的挡板,求电荷从开始运动到碰到挡板所需的时间。(保留三位有效数字)

⑴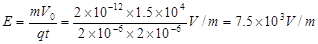 ⑵
⑵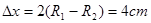 ⑶
⑶
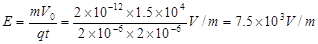 ⑵
⑵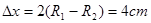 ⑶
⑶
⑴ 设粒子在电场中的加速度为a
由运动公式V0=at (1分)
由牛顿定律qE=ma (1分)
故电场强度大小:
 (2分)
(2分)
⑵ 如果粒子在匀强磁场B1=0.3T中作匀速圆周运动:
运动周期 (1分)
(1分)
运动轨道半径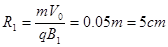 (1分)
(1分)
如果粒子在匀强磁场B2=0.5T中作匀速圆周运动:
运动周期 (1分)
(1分)
运动轨道半径 (1分)
(1分)
粒子进入磁场后在一个周期内的运动轨如图所示。(1分)
所以在一个周期内水平位移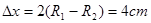 (2分)
(2分)
⑶ 在前15个周期内的水平位移S=15Δx=60cm (1分)
最后7.5m内的运动轨迹如图所示 (1分)
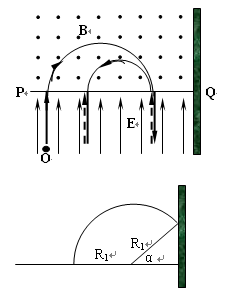

α=600 (1分)
最后7.5cm运动时间t3
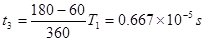 (1分)
(1分)
所以运动的总时间t

 (1分
(1分
由运动公式V0=at (1分)
由牛顿定律qE=ma (1分)
故电场强度大小:
 (2分)
(2分)⑵ 如果粒子在匀强磁场B1=0.3T中作匀速圆周运动:
运动周期
 (1分)
(1分)运动轨道半径
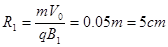 (1分)
(1分)如果粒子在匀强磁场B2=0.5T中作匀速圆周运动:
运动周期
 (1分)
(1分)运动轨道半径
 (1分)
(1分)粒子进入磁场后在一个周期内的运动轨如图所示。(1分)
所以在一个周期内水平位移
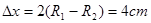 (2分)
(2分)⑶ 在前15个周期内的水平位移S=15Δx=60cm (1分)
最后7.5m内的运动轨迹如图所示 (1分)


α=600 (1分)
最后7.5cm运动时间t3
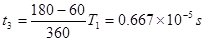 (1分)
(1分)所以运动的总时间t

 (1分
(1分
练习册系列答案
相关题目

 ´10-4s时刻,粒子的坐标。
´10-4s时刻,粒子的坐标。

 的带正电微粒,玻璃管置于一方向垂直水平面向下的匀强磁场中,磁感强度B=0.01T,磁场范围足够大,磁场中有一屏,距玻璃管口上方d= 60cm处。现让玻璃管水平向右匀速运动,当运动到如图虚线所示位置时,带电微粒恰好离开管口,再过
的带正电微粒,玻璃管置于一方向垂直水平面向下的匀强磁场中,磁感强度B=0.01T,磁场范围足够大,磁场中有一屏,距玻璃管口上方d= 60cm处。现让玻璃管水平向右匀速运动,当运动到如图虚线所示位置时,带电微粒恰好离开管口,再过 .带电微粒恰好到达屏上,且与屏相切。(一切摩擦均可忽略)求:
.带电微粒恰好到达屏上,且与屏相切。(一切摩擦均可忽略)求: