题目内容
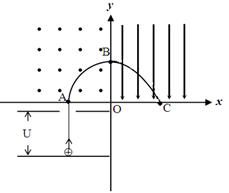
如图，在xoy直角坐标系中，在第三象限有一平行x轴放置的平行板电容器，板间电压U=1×102V。现有一质量m=1.0×10-12kg，带电量q=2.0×10-10C的带正电的粒子(不计重力)，从下极板处由静止开始经电场加速后通过上板上的小孔，垂直x轴从A点进入第二象限的匀强磁场中。磁场方向垂直纸面向外，磁感应强度B=1T。粒子在磁场中转过四分之一圆周后又从B点垂直y轴进入第一象限，第一象限中有平行于y轴负方向的匀强电场E，粒子随后经过x轴上的C点，已知OC=1m。求：
(1)粒子在磁场中做匀速圆周运动的半径r。
(2)第一象限中匀强电场场强E的大小。
(1)粒子在磁场中做匀速圆周运动的半径r。
(2)第一象限中匀强电场场强E的大小。
(1) 
(2) 
(2) ：
(1)设粒子飞出极板的速度为v，由动能定理：
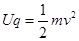(4分)
解得：
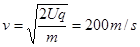(1分)
粒子在磁场中做匀速圆周运动，洛伦兹力提供向心力：
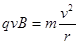(3分)
由以上可解得粒子做圆周运动的半径为：(2分)
(2)粒子从B点运动到C点的过程，
沿x轴方向有：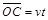
(2分)
沿y轴负方向有：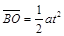
(2分)
其中BO=r(1分)又由牛顿第二定律：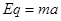
(1分)
由以上各式可解得：(2分)
(1)设粒子飞出极板的速度为v，由动能定理：
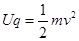(4分) 解得：
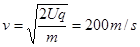(1分)粒子在磁场中做匀速圆周运动，洛伦兹力提供向心力：
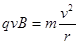(3分)由以上可解得粒子做圆周运动的半径为：
(2分)(2)粒子从B点运动到C点的过程，
沿x轴方向有：
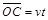(2分)沿y轴负方向有：
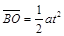(2分)其中BO=r(1分)又由牛顿第二定律：
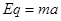(1分)由以上各式可解得：
(2分)
练习册系列答案
阅读快车系列答案
相关题目
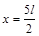的直线，磁场方向垂直纸面向外．一质量为m、带电荷量为+q的粒子从y轴上P点以初速度v0垂直y轴射人匀强电场，在电场力作用下从x轴上Q点以与x轴正方向成450角进入匀强磁场．已知OQ=l，不计粒子重力．求：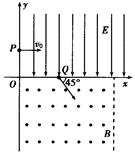
。现将小球从最低点A处由静止释放，则轻杆可以转过的最大角度为_____________。若在轻杆的中点施加一个始终垂直于杆的作用力F，F的大小始终保持为2mg，将小球从图中的B处由静止释放后，作用力F的最大功率Pm=_____________。
带电量为
的点电荷，在电场中的O点由静止释放，不计电荷的重力。粒子经t0=
第一次以
的速度通过PQ，并进入上方的磁场中。取磁场垂直向外方向为正，并以粒子第一次通过PQ时为t=0时刻。(本题中取
，重力加速度
)。试求：
时刻电荷与O点的水平距离；
射入，从O点沿着与y轴正方向成
夹角射出,求: