题目内容
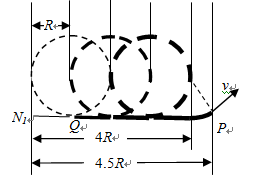
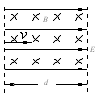
如图所示,宽度为d的竖直狭长区域内(边界为L1、L2),存在垂直纸面向里的匀强磁场和竖直方向上的周期性变化的电场(如图所示),电场强度的大小为E0,E>0表示电场方向竖直向上.t=0时,一带正电、质量为m的微粒从左边界上的N1点以水平速度v射入该区域,沿直线运动到Q点后,做二次完整的圆周运动(其轨迹恰好不穿出边界L1),以后可能重复该运动形式,最后从边界L2穿出.重力加速度为g,上述d、E0、m、v、g为已知量.
(1)求该微粒通过Q点瞬间的加速度;
(2)求磁感应强度B的大小和电场变化的周期T;
(3)若微粒做圆周运动的轨道半径为R,而d=4.5R,使微粒仍能按上述运动过程通过相应宽度的区域,求微粒所用的时间.
(1)求该微粒通过Q点瞬间的加速度;
(2)求磁感应强度B的大小和电场变化的周期T;
(3)若微粒做圆周运动的轨道半径为R,而d=4.5R,使微粒仍能按上述运动过程通过相应宽度的区域,求微粒所用的时间.

(1)a=2g(2)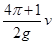 (3)
(3)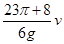
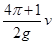 (3)
(3)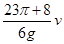
(1)(7分)微粒从N到Q,因做直线运动:mg+qE0=qvB (2分)
微粒做圆周运动,则mg=qE0 (2分)
在Q点: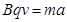 (2分) 所以:a=2g (1分 )
(2分) 所以:a=2g (1分 )
(2)(8分)由mg+qE0=qvB和mg=qE0则:B= (2分)
设微粒从N1运动到Q的时间为t1,做圆周运动的周期为t2,
因微粒恰好没穿出L1边界,则 R=vt1 (1分)
又qvB=m (1分) 2πR=vt2 (1分)
联立得电场变化的周期T=t1+2t2=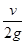 +2=
+2=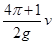 (3分)
(3分)
(3)(5分)若d=4.5R据题意可画出微粒如图的运动轨迹。
从图知:用(2)问的物理量可表示为“
t=3T+ t1+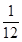 t2 =3(
t2 =3(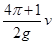 )+
)+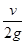 +
+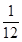
=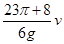
微粒做圆周运动,则mg=qE0 (2分)
在Q点:
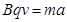 (2分) 所以:a=2g (1分 )
(2分) 所以:a=2g (1分 )(2)(8分)由mg+qE0=qvB和mg=qE0则:B= (2分)
设微粒从N1运动到Q的时间为t1,做圆周运动的周期为t2,
因微粒恰好没穿出L1边界,则 R=vt1 (1分)
又qvB=m (1分) 2πR=vt2 (1分)
联立得电场变化的周期T=t1+2t2=
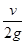 +2=
+2=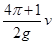 (3分)
(3分)(3)(5分)若d=4.5R据题意可画出微粒如图的运动轨迹。
从图知:用(2)问的物理量可表示为“
t=3T+ t1+
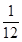 t2 =3(
t2 =3(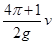 )+
)+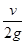 +
+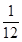
=
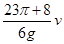


练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目



 带电量为
带电量为 的点电荷,在电场中的O点由静止释放,不计电荷的重力。粒子经t0=
的点电荷,在电场中的O点由静止释放,不计电荷的重力。粒子经t0= 第一次以
第一次以 的速度通过PQ,并进入上方的磁场中。取磁场垂直向外方向为正,并以粒子第一次通过PQ时为t=0时刻。(本题中取
的速度通过PQ,并进入上方的磁场中。取磁场垂直向外方向为正,并以粒子第一次通过PQ时为t=0时刻。(本题中取 ,重力加速度
,重力加速度 )。试求:
)。试求: 时刻电荷与O点的水平距离;
时刻电荷与O点的水平距离;



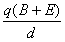
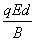
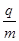 =1.0×108 C/kg,重力忽略不计,每个粒子通过电场区域的时间极短,电场可视为恒定不变。
=1.0×108 C/kg,重力忽略不计,每个粒子通过电场区域的时间极短,电场可视为恒定不变。