题目内容

如图，在xOy平面的第一、四象限内存在着方向垂直纸面向外、磁感应强度为B的匀强磁场，第四象限内存在方向沿-y方向、电场强度为E的匀强电场。从y轴上坐标为a的一点向磁场区发射速度大小不等的带正电同种粒子，速度方向范围是与+y方向成30°～150°，且在xOy平面内。结果所有粒子经过磁场偏转后都垂直打到x轴上，然后进入第四象限的匀强电场区。已知带电粒子电量为q，质量为m，粒子的重力及粒子间相互作用不计。求：

（1）垂直y轴方向射入磁场粒子运动的速度大小v1；
（2）求粒子在第Ⅰ象限的磁场中运动的最长时间与最短时间差。；
（3）从x轴上x=（-1）a点射人第四象限的粒子穿过电磁场后经过y轴上y=-b的点，求该粒子经过y=-b点的速度大小。

v=qBa/m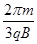    

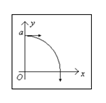
解析试题分析：（1）如图所示，粒子运动的轨迹圆心在坐标原点，轨道半径R=a，（1分）
有qvB=mv2/R，（2分）
v=qBa/m（1分）
（2）最长时间对应粒子初速度与y轴正方向夹角30°，转过150°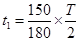
 （2分）
最短时间对应粒子初速度与y轴负方向夹角30°，转过30°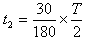
 （2分）
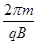T=   （1分）
故时间差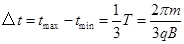   （1分）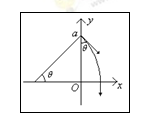

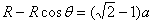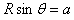（3）粒子射出时与y轴负方向夹角θ，则有     （1分）
     （1分）
得到：，
速度v0为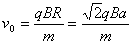   （1分）
到达y轴速度v，则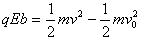          （ 2分）
      （2分）
考点：本题考查带点粒子在电场磁场中运动。

练习册系列答案
相关题目

如右图所示为圆柱形区域的横截面，在该区域加沿圆柱轴线方向的匀强磁场．带电粒子(不计重力)第一次以速度沿截面直径入射，粒子飞入磁场区域时，速度方向偏转60°角；该带电粒子第二次以速度从同一点沿同一方向入射，粒子飞出磁场区域时，速度方向偏转90°角．则带电粒子第一次和第二次在磁场中运动的(　　)

A．半径之比为 B．速度之比为
C．时间之比为2∶3 D．时间之比为3∶2

（18分）如图所示，圆心为原点、半径为R的圆将xOy平面分为两个区域，即圆内区域Ⅰ和圆外区域Ⅱ。区域Ⅰ内有方向垂直于xOy平面的匀强磁场B1。平行于x轴的荧光屏垂直于xOy平面，放置在坐标y＝－2.2R的位置。一束质量为m、电荷量为q、动能为E0的带正电粒子从坐标为（－R，0）的A点沿x正方向射入区域Ⅰ，当区域Ⅱ内无磁场时，粒子全部打在荧光屏上坐标为（0，－2.2R）的M点，且此时，若将荧光屏沿y轴负方向平移，粒子打在荧光屏上的位置不变。若在区域Ⅱ内加上方向垂直于xOy平面的匀强磁场B2，上述粒子仍从A点沿x轴正方向射入区域Ⅰ，则粒子全部打在荧光屏上坐标为（0.4R，－2.2R）的 N点。求：

（1）打在M点和N点的粒子运动速度v1、v2的大小。
（2）在区域Ⅰ和Ⅱ中磁感应强度B1、B2的大小和方向。
（3）若将区域Ⅱ中的磁场撤去，换成平行于x轴的匀强电场，仍从A点沿x轴正方向射入区域Ⅰ的粒子恰好也打在荧光屏上的N点，则电场的场强为多大？

（20分）如图所示，xOy坐标系的第一象限内，有一边界线OA与y轴的夹角∠AOy=45O，边界线的上方与下方分别存在垂直纸面向外与向里的匀强磁场，磁感应强度大小均为B=0.25T．一束带电量q=8.0×10-19C、质量 m=8.0×10-26kg的正离子以v=5×105m/s从y轴上坐标为（0，0.4m）的Q点垂直y轴射入磁场区。求：

（1）离子在磁场中做圆周运动的半径和周期；
（2）现只改变B的大小，使离子不经过OA边界而直接从y轴离开磁场区域，则B应满足什么条件？
（3）若B=0.125T，且从离子经过Q点开始计时，则离子在哪些时刻恰好经过OA边界？

如图所示，坐标系xoy在竖直平面内，y轴的正方向竖直向上，y轴的右侧广大空间存在水平向左的匀强电场E1=2N/C，y轴的左侧广大空间存在匀强电场，磁场方向垂直纸面向外，B=1T，电场方向竖直向上，E2=2N/C。t=0时刻，一个带正电的质点在O点以v=2m/s的初速度沿着与x轴负方向成450角射入y轴的左侧空间，质点的电量为q=106C，质量为m=2×10-7kg，重力加速度g=10m/s2。求：

（1）质点从O点射入后第一次通过y轴的位置；
（2）质点从O点射入到第二次通过y轴所需时间；
（3）质点从O点射入后第四次通过y轴的位置。

（18分）如图所示，在第一、二象限存在场强均为E的匀强电场，其中第一象限的匀强电场的方向沿x轴正方向，第二象限的电场方向沿x轴负方向。在第三、四象限矩形区域ABCD内存在垂直于纸面向外的匀强磁场，矩形区域的AB边与x轴重合。M点是第一象限中无限靠近y轴的一点，在M点有一质量为m、电荷量为e的质子，以初速度v0沿y轴负方向开始运动，恰好从N点进入磁场，若OM＝2ON，不计质子的重力，试求：

（1）N点横坐标d；
（2）若质子经过磁场最后能无限靠近M点，则矩形区域的最小面积是多少；
（3）在（2）的前提下，该质子由M点出发返回到无限靠近M点所需的时间。

如图所示，竖直面内有一倒立等边三角形OMN区域，连长为L，MN边是水平的。在该区域有一垂直纸面向外磁感应强度为B的匀强磁场。在同一竖直面内有一束质量为m、电荷量为q、速度大小不同的带正电粒子从N点沿NM方向射入该磁场区域（可认为能发生偏转）。过O点作与MN边平行的直线作为X坐标轴，且O点为X坐标轴的原点。不计粒子的重力及粒子间的相互作用力，试求：

⑴射到X坐标轴上的O点的粒子速度大小；
⑵垂直OM边射出的粒子与X坐标轴的交点位置；
⑶粒子在磁场中运动的时间和速度的关系。

（22分）如图所示，半径足够大的两半圆形区域I和II中存在与纸面垂直的匀强磁场，两半圆形的圆心分别为O、O’，两条直径之间有一宽度为d的矩形区域，区域内加上电压后形成一匀强电场。一质量为m、电荷量为+q的带电粒子（不计重力），以初速度v0从M点沿与直径成30o角的方向射入区域I，而后从N点沿与直径垂直的方向进入电场，N点与M点间的距离为L0，粒子第一次离开电场时的速度为2v0，随后将两直径间的电压调为原来的2倍，粒子又两进两出电场，最终从P点离开区域II。已知P点与圆心为O’的直径间的距离为L，与最后一次进入区域II时的位置相距L，求：
（1）区域I内磁感应强度B1的大小与方向
（2）矩形区域内原来的电压和粒子第一次在电场中运动的时间；
（3）大致画出粒子整个运动过程的轨迹，并求出区域II内磁场的磁感应强度B2的大小；
（4）粒子从M点运动到P点的时间。

(16分)如图所示，在矩形区域ABCD内有垂直于纸面向外的匀强磁场，磁感应强度大小为B=5.0×10—2T，矩形区域AD长为m，AB宽为0.2 m，在AD边中点O处有一放射源，某时刻，放射源沿纸面向磁场中各方向均匀地辐射出速率均为v=2×l06 m/s的某种带正电粒子，带电粒子质量m=1.6×10-27 kg，电荷量为q=+3.2×l0-19C（不计粒子重力），求：

(1)带电粒子在磁场中做圆周运动的半径；
(2)从BC边界射出的粒子中，在磁场中运动的最短时间；
(3)分别从BC边界和CD边界射出粒子数目的比值。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网