题目内容
(22分)如图所示,半径足够大的两半圆形区域I和II中存在与纸面垂直的匀强磁场,两半圆形的圆心分别为O、O’,两条直径之间有一宽度为d的矩形区域,区域内加上电压后形成一匀强电场。一质量为m、电荷量为+q的带电粒子(不计重力),以初速度v0从M点沿与直径成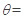 30o角的方向射入区域I,而后从N点沿与直径垂直的方向进入电场,N点与M点间的距离为L0,粒子第一次离开电场时的速度为2v0,随后将两直径间的电压调为原来的2倍,粒子又两进两出电场,最终从P点离开区域II。已知P点与圆心为O’的直径间的距离为L,与最后一次进入区域II时的位置相距
30o角的方向射入区域I,而后从N点沿与直径垂直的方向进入电场,N点与M点间的距离为L0,粒子第一次离开电场时的速度为2v0,随后将两直径间的电压调为原来的2倍,粒子又两进两出电场,最终从P点离开区域II。已知P点与圆心为O’的直径间的距离为L,与最后一次进入区域II时的位置相距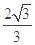 L,求:
L,求:
(1)区域I内磁感应强度B1的大小与方向
(2)矩形区域内原来的电压和粒子第一次在电场中运动的时间;
(3)大致画出粒子整个运动过程的轨迹,并求出区域II内磁场的磁感应强度B2的大小;
(4)粒子从M点运动到P点的时间。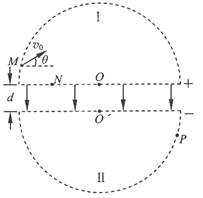
(1) ;B1方向垂直于纸面向外(2)
;B1方向垂直于纸面向外(2) ;
; (3)
(3)
(4)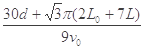
解析试题分析:(1)粒子在Ⅰ内速度方向改变了120°,由几何关系知,轨迹对应的圆心角
α=120°

由

B1方向垂直于纸面向外
(2)粒子第一次在电场中运动由动能定理: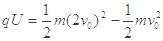
∴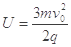

∴

(3)粒子第二次进入电场中,设粒子运动x距离时速度为0

∴粒子不能进入区域Ⅰ,而是由速度为0开始反向加速进入区域Ⅱ粒子整个运动过程的大致轨迹如图所示。…(1分)
对粒子在区域Ⅱ内运动的最后一段轨迹:
β=60°,最后一段轨迹对应的圆心角φ=60°
∴
由

(4)在区域Ⅰ中运动时间t0
粒子第二次在电场中运动的时间t2
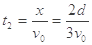
从粒子第二次进入电场到最终离开区域Ⅱ,粒子在电场中运动的总时间
t2′=4t2=
粒子在区域Ⅱ的所有圆弧上运动的时间:
粒子从M点运动到P点的时间:
t= t0+ t1+ t2′+ t3=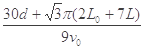
考点:带电粒子在匀强电场中的加速;带电粒子在匀强磁场中的圆周运动。

 阅读快车系列答案
阅读快车系列答案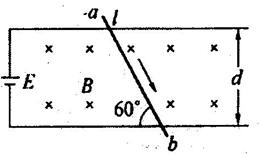
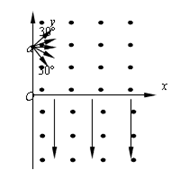
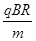 。已知a在离开圆形区域I后,从某点P进入区域II。该粒子a离开区域II时,速度方向与x轴正方向的夹角为30°;此时,另一质量和电荷量均与a相同的粒子b从P点进入区域II,其速度沿x轴正向,大小是粒子a的
。已知a在离开圆形区域I后,从某点P进入区域II。该粒子a离开区域II时,速度方向与x轴正方向的夹角为30°;此时,另一质量和电荷量均与a相同的粒子b从P点进入区域II,其速度沿x轴正向,大小是粒子a的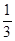 。不计重力和两粒子之间的相互作用力。求:
。不计重力和两粒子之间的相互作用力。求: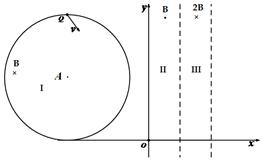
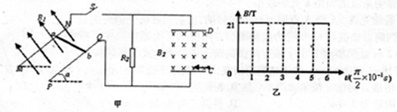
 周期性变化,使平行金属板M、N间获得如图乙的周期性变化的电压。M、N中心的小孔P、Q的连线与金属板垂直,N板右侧匀强磁场(磁感应强度为B2)的区域足够大。绝缘档板C垂直N板放置,距小孔Q点的距离为h。现使置于P处的粒子源持续不断地沿PQ方向释放出质量为m、电量为q的带正电粒子(其重力、初速度、相互间作用力忽略不计)。
周期性变化,使平行金属板M、N间获得如图乙的周期性变化的电压。M、N中心的小孔P、Q的连线与金属板垂直,N板右侧匀强磁场(磁感应强度为B2)的区域足够大。绝缘档板C垂直N板放置,距小孔Q点的距离为h。现使置于P处的粒子源持续不断地沿PQ方向释放出质量为m、电量为q的带正电粒子(其重力、初速度、相互间作用力忽略不计)。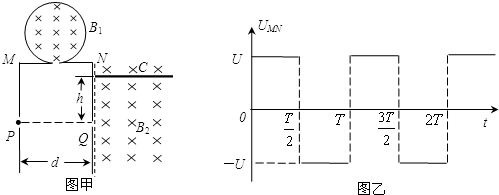
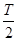 时间内,B1大小按
时间内,B1大小按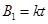 的规律增大,此时M板电势比N板高,请判断此时B1的方向。试求,圆形导线框的面积S多大才能使M、N间电压大小为U?
的规律增大,此时M板电势比N板高,请判断此时B1的方向。试求,圆形导线框的面积S多大才能使M、N间电压大小为U?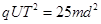 ,则在什么时刻由P处释放的粒子恰能到达Q孔但不会从Q孔射入磁场?结果用周期T的函数表示。
,则在什么时刻由P处释放的粒子恰能到达Q孔但不会从Q孔射入磁场?结果用周期T的函数表示。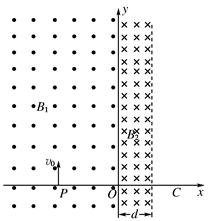
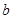 ,-
,-
 T,粒子的荷质比
T,粒子的荷质比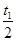 C/kg,不计粒子的重力。问:
C/kg,不计粒子的重力。问: