��Ŀ����
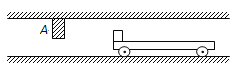
����Ŀ����ͼ��ʾ����ˮƽ������һ���ɣ��������ǽ��������O��Ϊ����ԭ��λ�ã�O�����ˮƽ��⻬��ˮƽ��OP��L=1m��P���Ҳ�һ��ˮƽ����ɦ�=30����㹻���Ĵ��ʹ���ˮƽ����P��ƽ�����ӣ�Ƥ������ʱ��ת������Ϊ3m/s��һ����Ϊ1kg����Ϊ�ʵ�����Aѹ���������뵯�ɲ�˨������ʹ���ɻ�õ�������Ep=9J�������OP�ζ�Ħ�����ئ�1=0��1����һ��A��ȫ��ͬ�����Bͣ��P�㣬B�봫�ʹ��Ķ�Ħ�����ئ�2=![]() �����ʹ��㹻����A��B����ײʱ�䲻�ƣ�����A��B�����ٶȣ��������ٶ�g=10m/s2�����ͷ�A����
�����ʹ��㹻����A��B����ײʱ�䲻�ƣ�����A��B�����ٶȣ��������ٶ�g=10m/s2�����ͷ�A����
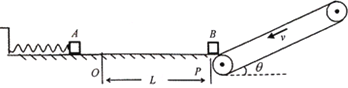
��1�����A��B��һ����ײǰ˲�䣬A������v0��
��2����A��B��һ����ײ�ڶ�����ײǰ��B�봫�ʹ�֮������Ħ����������������
��3��A��B�ܹ���ײ���ܴ�����
���𰸡���1�����A��B��һ����ײǰ˲�䣬A������Ϊ4m/s��
��2����A��B��һ����ײ�ڶ�����ײǰ��B�봫�ʹ�֮������Ħ��������������Ϊ12��25J��
��3��A��B�ܹ���ײ���ܴ���Ϊ6����
��������
�����������1�����ͷŵ���B��ײǰ�Ĺ��̣���A��ϵͳ���ù��ܹ�ϵ��ʽ������������A��B��һ����ײǰ���ٶȣ�
��2�����ݶ����غ㶨�ɺͻ�е���غ㶨���������A��B���ٶ���B����ٶȺ�����B��Ƥ���������ȼ����˶�ֱ���ٶ�Ϊ�㣬Ȼ���������ȼ����˶�������ţ�ٵڶ����ɺ��˶�ѧ��ʽ��ϣ��ֶ����ʱ���λ�ƣ�����Ϲ�ʽQ=f��S���������
��3��B��A�ڶ�����ײ�������ٶ��ٴλ������˺�A�����˶��ٷ���ʱ��B��ײ��B��Ƥ���������˶���ԭ�ٷ��أ��ظ���һ����ֱ�����߲�����ײ��ÿһ�ι�������ʧ�Ļ�е��Ϊ2��1mgl�������������������غ���ʽ���A��B��ײ�Ĵ�����
�⣺��1�����������Ϊm��A��B��һ����ǰ���ٶ�Ϊv0����![]()
��ã�v0=4m/s
��2����A��B��һ����ײ����ٶȷֱ�ΪvA��vB����vA=0��vB=4m/s������B�ش��ʹ������ȼ����˶�ֱ���ٶ�Ϊ�㣬���ٶȴ�С��Ϊa1����mgsin��+��2mgcos��=ma1����ã�a1=gsin��+��2gcos��=10m/s2
�˶���ʱ��![]()
�![]() =0��8m
=0��8m
�˹�������˶�·�̡�s1=vt1+x1=2m
�˺�B������٣����ٶ���Ϊa1���봫�ʹ����ٺ������˶�ֱ����A�ٴ���ײ������ʱ��Ϊ![]() =0��3s
=0��3s
λ��Ϊ![]()
�˹�������˶�·�̡�s2=vt2��x2=0��45m
ȫ��������Q=��2mgcos������s1+��s2��=12��25J
��3��B��A�ڶ�����ײ�������ٶ��ٴλ������˺�A�����˶��ٷ�����B��ײ��B�ش��ʹ������˶��ٴη��أ�ÿ�������ٴ���ǰ������ȣ��ظ���һ����ֱ�����߲�����ײ��
���A��B�͵�����ɵ�ϵͳ���ӵڶ�����ײ������ײ��![]() =2n��1mgL
=2n��1mgL
��õڶ�����ײ���ظ��Ĺ�����Ϊn=2��25
������ײ�ܴ���ΪN=2+2n=6��5=6����ȡ������