题目内容
【题目】在“研究平抛物体的运动”实验中:
(1)将斜槽放在实验桌面上,实验前要检查斜槽的末端是否水平,这是为了;
(2)在记录小球轨迹的白纸上,记录了竖直向下的y轴方向和水平x轴方向以及轨迹上三个点A,B,C的位置,如图所示,测量出:A、B和B、C间水平距离xAB=xBC=15cm,竖直方向的距离yAB=15cm,yBC=25cm,由此可以计算出小球做平抛运动的初速度大小v0= , 小球通过B点的瞬时速度的大小vB= , 方向(取g=10m/s2)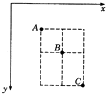
【答案】
(1)保证小球做平抛运动
(2)1.5m/s;2.5m/s;水平方向成53°夹角
【解析】解:(1)研究平抛运动的实验很关键的地方是要保证小球能够水平飞出,只有水平飞出,小球才做平抛运动,所以斜槽末端需水平.(2)因为平抛运动在水平方向上做匀速直线运动,可知AB、BC的时间间隔相等.
在竖直方向上,根据匀变速直线运动的推论有:yBC﹣yAB=gT2 ,
解得:T= 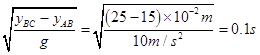
水平方向匀速直线运动,因此有:![]()
某段时间内的平均速度等于中间时刻的瞬时速度,则B点竖直方向上的分速度,则:![]()
因此B点的速度为: ![]()
与水平方向的夹角为θ,则有:![]() ,则有:θ=53°,即速度方向与水平方向成53°夹角.
,则有:θ=53°,即速度方向与水平方向成53°夹角.
所以答案是:(1)保证小球做平抛运动;(2)1.5m/s; 2.5m/s,水平方向成53°夹角.
【考点精析】解答此题的关键在于理解平抛运动的相关知识,掌握特点:①具有水平方向的初速度;②只受重力作用,是加速度为重力加速度g的匀变速曲线运动;运动规律:平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目