题目内容
3. 如图所示,点电荷A的电荷量为Q,点电荷B的电荷量为q,相距为r.已知静电力常量为k,求:
如图所示,点电荷A的电荷量为Q,点电荷B的电荷量为q,相距为r.已知静电力常量为k,求:(1)电荷A与B之间的库仑力大小;
(2)电荷A、B在它们连线中点处产生的电场强度;
(3)移去电荷B后,电荷A在原来电荷B所在处产生的电场强度.
分析 (1)根据库仑定律求电荷间的库仑力大小.
(2)依据点电荷场强公式E=k$\frac{Q}{{r}^{2}}$求出两个电荷A与B在它们的连线中点处的场强,然后由矢量合成的方法即可求出中点的合场强.
(3)某点的电场强度是由电场本身决定的,所以移去电荷B后,电荷A在原电荷B所在处产生的电场强度大小不变.
解答 解:(1)由库仑定律得:
电荷A与B之间的库仑力大小 F=k$\frac{Qq}{{r}^{2}}$
(2)电荷A在它们连线中点处产生的电场强度方向水平向右,大小为 EA=k$\frac{Q}{(\frac{r}{2})^{2}}$
电荷B在它们连线中点处产生的电场强度方向水平向右,大小为 EB=k$\frac{q}{(\frac{r}{2})^{2}}$
则电荷A、B在它们连线中点处产生的电场强度大小 E=EA+EB
联立解得 E=$\frac{4k(Q+q)}{{r}^{2}}$,方向水平向右.
(3)某点的电场强度是由电场本身决定的,所以移去电荷B后,电荷A在原电荷B所在处产生的电场强度大小为 E=k$\frac{Q}{{r}^{2}}$,方向水平向右.
答:
(1)电荷A与B之间的库仑力大小是k$\frac{Qq}{{r}^{2}}$;
(2)电荷A、B在它们连线中点处产生的电场强度是$\frac{4k(Q+q)}{{r}^{2}}$,方向水平向右;
(3)移去电荷B后,电荷A在原来电荷B所在处产生的电场强度是k$\frac{Q}{{r}^{2}}$,方向水平向右.
点评 本题的关键要掌握库仑定律和点电荷场强公式E=k$\frac{Q}{{r}^{2}}$,知道空间任意一点的场强是各个点电荷产生的场强的叠加,运用矢量合成法则求合场强.

练习册系列答案
相关题目
11.A、B两球用长为L的细线相连,现用提着B从一定高处由静止释放,A、B两球落地时间差为△t1,速度差为△v1.若再从稍高处自由释放,两球落地时间差为△t2,速度差为△v2,不计空气阻力,则( )
| A. | △t1<△t2 | B. | △t1>△t2 | C. | △v1>△v2 | D. | △v1<△v2 |
18. 如图所示,质量为M木块静止在光滑的水平面上,一颗质量为m的子弹水以速度υ0平射入木块并留在木块中,木块获得的速度为υ1,子弹受到的平均阻力为f,射入深度为d,此过程中木块位移为s,下列说法正确的是( )
如图所示,质量为M木块静止在光滑的水平面上,一颗质量为m的子弹水以速度υ0平射入木块并留在木块中,木块获得的速度为υ1,子弹受到的平均阻力为f,射入深度为d,此过程中木块位移为s,下列说法正确的是( )
 如图所示,质量为M木块静止在光滑的水平面上,一颗质量为m的子弹水以速度υ0平射入木块并留在木块中,木块获得的速度为υ1,子弹受到的平均阻力为f,射入深度为d,此过程中木块位移为s,下列说法正确的是( )
如图所示,质量为M木块静止在光滑的水平面上,一颗质量为m的子弹水以速度υ0平射入木块并留在木块中,木块获得的速度为υ1,子弹受到的平均阻力为f,射入深度为d,此过程中木块位移为s,下列说法正确的是( )| A. | 子弹损失的动能等于fd | |
| B. | 子弹损失的动能为$\frac{1}{2}$mυ02 | |
| C. | 子弹、木块组成的系统损失的动能等于fd | |
| D. | 子弹、木块组成的系统损失的动能为$\frac{1}{2}$(m+M)υ02-$\frac{1}{2}$(m+M)υ12 |
15.下列各组选项中只含一个标量的选项是( )
| A. | 平均速度、质量、加速度 | B. | 瞬时速度、速率、路程 | ||
| C. | 平均速率、时间、温度 | D. | 频率、位移、速度 |
13. 如图所示,空心导体上方有一靠得很近的带电体,带有正电荷.有一束带负电的小液滴(重力不能忽略),以速度v水平飞入空心导体腔内,则小液滴的运动情况是( )
如图所示,空心导体上方有一靠得很近的带电体,带有正电荷.有一束带负电的小液滴(重力不能忽略),以速度v水平飞入空心导体腔内,则小液滴的运动情况是( )
 如图所示,空心导体上方有一靠得很近的带电体,带有正电荷.有一束带负电的小液滴(重力不能忽略),以速度v水平飞入空心导体腔内,则小液滴的运动情况是( )
如图所示,空心导体上方有一靠得很近的带电体,带有正电荷.有一束带负电的小液滴(重力不能忽略),以速度v水平飞入空心导体腔内,则小液滴的运动情况是( )| A. | 匀速直线运动 | B. | 变速直线运动 | ||
| C. | 向上偏转的曲线运动 | D. | 向下偏转的曲线运动 |

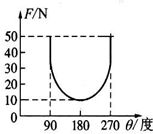 作用在同一质点上的两个力的合力F随两个分力夹角大小的变化情况如图所示,则两力的大小分别是40N和30N.
作用在同一质点上的两个力的合力F随两个分力夹角大小的变化情况如图所示,则两力的大小分别是40N和30N.