题目内容
【题目】如图所示,一条河宽为60m,水流速度恒为5m/s,现要将小船上的货物由此岸的A处沿直线送达正对岸下游45m处的B处。已知小船的速度最大可达5m/s,取sin37°=0.6,cos37°=0.8,g=10m/s2。
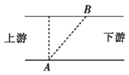
(1)如果小船以最小速度航行,求船速v1的大小和方向;
(2)如果要使小船在最短时间内抵达B处,求船速v2的取值和方向;
(3)求小船运动的最短时间t0。
【答案】(1)如果小船以最小速度航行,船速v1的大小为4m/s和方向与河岸夹角为37°指向上游;(2)如果要使小船在最短时间内抵达B处,船速v2的取值为5m/s和方向指向上游,与河岸成74°;(3)小船运动的最短时间是12.5s。
【解析】
(1)为使小船抵达B处,小船的实际航线须沿题目图中的AB方向,即合速度方向沿AB方向,设AB与河岸的夹角为θ,由三角形法则可得:
v1=v水sinθ
方向与河岸夹角为37°指向上游;
由几何关系得:AB=75m,有:sinθ=0.8
解得:
v1=4m/s
(2)为使小船能在最短时间内抵达B处,小船应该以最大速度航行,即v2=5m/s,并使合速度的方向仍沿AB方向;由于船速和水速大小相等,所以AB的方向是在两个速度的角平分线上,v2的方向与河岸成2θ角,由几何关系得2θ=106°,即船速指向上游,与河岸成74°。
(3)小船运动的合速度为:
v=2v2cosθ=2×5×0.6m/s=6m/s
所以小船运动的最短时间为:
t0=![]() =
=![]() s=12.5s。
s=12.5s。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目