题目内容
（12分）如图，竖直放置的斜面AB的下端与光滑的圆弧轨道BCD的B端相切，C为圆弧最低点,圆弧半径为R，圆心O与A、D在同一水平面上，∠COB=30°。现有一个质量为m的小物体从A点无初速滑下，已知小物体与斜面间的动摩擦因数为m，
求：（1）小物体在斜面上滑行的总路程；
（2）小物体通过C点时，对C点的最大压力和最小压力。
（1）s=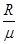
（2）最大压力和最小压力3（1－µ）mg 和
解析:解：
（1）小物体最终将在以过圆心的半径两侧q 范围内运动，由动能定理得
mgRcosq－mmgscosq =0 （2分）
解得 ：s=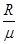 （1分）
（2）小物体第一次到达最低点时对C点的压力最大；
（1分）
由动能定理得： （2分）
解得：Nm=mg（3－2µcosqctgq）= 3（1－µ）mg （2分）
当小物体最后在BCE（E在C点左侧与B等高）圆弧上运动时，通过C点时对轨道压力最小.
Nn－mg =m （1分）
mgR(1－cosq) =（2分）
解得：N n= mg (3－2cosq)= （1分）
练习册系列答案
春雨教育同步作文系列答案
相关题目
附加题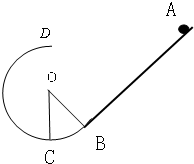
如图，竖直放置的斜面下端与光滑的圆弧轨道BCD的B端相切，圆弧半径为R，∠COB=θ，斜面倾角也为θ，现有一质量为m的小物体从斜面上的A点无初速滑下，且恰能通过光滑圆形轨道的最高点D．已知小物体与斜面间的动摩擦因数为μ，
（2010?济南一模）如图，竖直放置的斜面CD的下端与光滑圆弧轨道ABC的C端相切，圆弧半径为R，圆心与A、D在同一水平面上，∠COB=45°，现将一个质量为m的小物块从A点上方距A竖直高度为h=0.5R的位置无初速释放，小物块从A点进入轨道运动至斜面上D点后返回．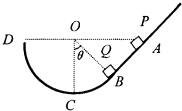
如图，竖直放置的斜面AB的下端与光华圆弧轨道BCD的B端相切，圆弧半径为R，圆心与A、D在同一水平面上，∠COB=θ，现有一个质量为m的小物块P从斜面上的A点无初速滑下，与位于B点的另外一个质量也为m的小物块Q碰撞，碰后，两个物块粘连在一起，已知两个小物块与斜面间的动摩擦因数均为μ，求：