题目内容
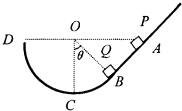 如图,竖直放置的斜面AB的下端与光华圆弧轨道BCD的B端相切,圆弧半径为R,圆心与A、D在同一水平面上,∠COB=θ,现有一个质量为m的小物块P从斜面上的A点无初速滑下,与位于B点的另外一个质量也为m的小物块Q碰撞,碰后,两个物块粘连在一起,已知两个小物块与斜面间的动摩擦因数均为μ,求:
如图,竖直放置的斜面AB的下端与光华圆弧轨道BCD的B端相切,圆弧半径为R,圆心与A、D在同一水平面上,∠COB=θ,现有一个质量为m的小物块P从斜面上的A点无初速滑下,与位于B点的另外一个质量也为m的小物块Q碰撞,碰后,两个物块粘连在一起,已知两个小物块与斜面间的动摩擦因数均为μ,求:(1)粘连体在斜面上运动的路程.
(2)粘连体通过C点时,对C点的最大压力和最小压力.(两个小物体均可视为质点)
分析:(1)由几何知识得知,斜面的倾角等于θ.物体从A点无初速度滑下后,由于克服摩擦力做功,物体在斜面上运动时机械能不断减小,到达的最大高度越来越小,最终在BE圆弧上来回运动,到达B点的速度为零.物体在斜面上运动时摩擦力大小为μ2mgcosθ,总是做负功,滑动摩擦力做的总功与总路程成正比,根据动能定理求解总路程.
(2)当物体第一次经过C点时,速度最大,对C点的压力最大,当最后稳定后,物体在B点之下运动时,经过C点时速度最小,物体对C点的压力最小,根据动能定理求出最大速度和最小速度,再由牛顿运动定律求解最大压力和最小压力.
(2)当物体第一次经过C点时,速度最大,对C点的压力最大,当最后稳定后,物体在B点之下运动时,经过C点时速度最小,物体对C点的压力最小,根据动能定理求出最大速度和最小速度,再由牛顿运动定律求解最大压力和最小压力.
解答:解:(1)P滑到B点过程中重力和摩擦力做功,物体的动能增大:
由几何关系知,P下滑的高度:h=Rcosθ;斜面与水平面的夹角为θ;
设B点以上的斜面长为s,则:s=
=
由动能定理得:mgh-μmgscosθ=
mv2
联立以上各方程,解得:v=
到B点与Q发生完全碰撞,由于碰撞的时间短,可以认为碰撞的过程中动量守恒,则:mv=2mv′
由于克服摩擦力做功,物体在斜面上运动时机械能不断减小,到达的最大高度越来越小,
最终粘连体在圆弧上角度为2θ范围内做往复运动,故最终粘连体在B点速度为0
由动能定理:
?2mv′2=μ?2mcosθ?S0
代入数据解得:S0=
(2)第一次往返C点时压力最大,设为F1,对于PQ整体,B→C过程机械能守恒:
×2mv′2+2mgR(1-cosθ)=
×2m
…①
在C点:F1-2mg=2m?
…②
代入数据解得:F1=2mg+4mg(1-cosθ)+
×
×2gR(sinθ-μcosθ)?cotθ=6mg-3mgcosθ-μmg
当物体不能冲出B点时,再经过C点时的压力最小,设在C点的最小压力为F2.
2mgR(1-cosθ)=
×2m
…③
在C点:F2-2mg=2m?
…④
代入数据解得:F2=6mg-4mgcosθ
答:(1)粘连体在斜面上运动的路程为S0=
;
(2)粘连体通过C点时,对C点的最大压力为6mg-3mgcosθ-μmg
,最小压力为:6mg-4mgcosθ.
由几何关系知,P下滑的高度:h=Rcosθ;斜面与水平面的夹角为θ;
设B点以上的斜面长为s,则:s=
| h |
| sinθ |
| R |
| tanθ |
由动能定理得:mgh-μmgscosθ=
| 1 |
| 2 |
联立以上各方程,解得:v=
|
到B点与Q发生完全碰撞,由于碰撞的时间短,可以认为碰撞的过程中动量守恒,则:mv=2mv′
由于克服摩擦力做功,物体在斜面上运动时机械能不断减小,到达的最大高度越来越小,
最终粘连体在圆弧上角度为2θ范围内做往复运动,故最终粘连体在B点速度为0
由动能定理:
| 1 |
| 2 |
代入数据解得:S0=
| R(sinθ-μcosθ) |
| 4μtanθ |
(2)第一次往返C点时压力最大,设为F1,对于PQ整体,B→C过程机械能守恒:
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 c |
在C点:F1-2mg=2m?
| ||
| R |
代入数据解得:F1=2mg+4mg(1-cosθ)+
| 2m |
| R |
| 1 |
| 4 |
| cos2θ |
| sinθ |
当物体不能冲出B点时,再经过C点时的压力最小,设在C点的最小压力为F2.
2mgR(1-cosθ)=
| 1 |
| 2 |
| v | 2 C1 |
在C点:F2-2mg=2m?
| ||
| R |
代入数据解得:F2=6mg-4mgcosθ
答:(1)粘连体在斜面上运动的路程为S0=
| R(sinθ-μcosθ) |
| 4μtanθ |
(2)粘连体通过C点时,对C点的最大压力为6mg-3mgcosθ-μmg
| cos2θ |
| sinθ |
点评:本题是动能定理与牛顿运动定律的综合应用,关键是分析物体的运动过程,抓住滑动摩擦力做功与路程有关这一特点.

练习册系列答案
相关题目
 附加题
附加题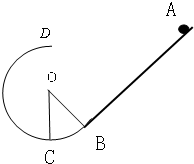 如图,竖直放置的斜面下端与光滑的圆弧轨道BCD的B端相切,圆弧半径为R,∠COB=θ,斜面倾角也为θ,现有一质量为m的小物体从斜面上的A点无初速滑下,且恰能通过光滑圆形轨道的最高点D.已知小物体与斜面间的动摩擦因数为μ,
如图,竖直放置的斜面下端与光滑的圆弧轨道BCD的B端相切,圆弧半径为R,∠COB=θ,斜面倾角也为θ,现有一质量为m的小物体从斜面上的A点无初速滑下,且恰能通过光滑圆形轨道的最高点D.已知小物体与斜面间的动摩擦因数为μ, (2010?济南一模)如图,竖直放置的斜面CD的下端与光滑圆弧轨道ABC的C端相切,圆弧半径为R,圆心与A、D在同一水平面上,∠COB=45°,现将一个质量为m的小物块从A点上方距A竖直高度为h=0.5R的位置无初速释放,小物块从A点进入轨道运动至斜面上D点后返回.
(2010?济南一模)如图,竖直放置的斜面CD的下端与光滑圆弧轨道ABC的C端相切,圆弧半径为R,圆心与A、D在同一水平面上,∠COB=45°,现将一个质量为m的小物块从A点上方距A竖直高度为h=0.5R的位置无初速释放,小物块从A点进入轨道运动至斜面上D点后返回.