题目内容
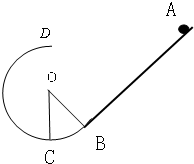如图，竖直放置的斜面下端与光滑的圆弧轨道BCD的B端相切，圆弧半径为R，∠COB=θ，斜面倾角也为θ，现有一质量为m的小物体从斜面上的A点无初速滑下，且恰能通过光滑圆形轨道的最高点D．已知小物体与斜面间的动摩擦因数为μ，求：（1）AB长度l应该多大．
（2）小物体第一次通过C点时对轨道的压力多大．
分析：（1）根据牛顿第二定律列出重力提供向心力的表达式，再由动能定理结合几何关系即可求解；
（2）由机械能守恒定律与牛顿第二定律联合即可求解．
（2）由机械能守恒定律与牛顿第二定律联合即可求解．
解答：解：（1）因恰能过最高点C，则有mg=m
又因f=μN=μmgcosθ，
物体从A运动到C全程，由动能定理
可得：mg（lsinθ-R-Rcosθ）-fl=
mv2-0
联立求得：l=
（2）物体从C运动到D的过程，设C点速度为vc，由机械能守恒定律：
mvc2=
mv2+mg2R（4 ）
物体在C点时：N-mg=
（5）
联合求得：N=6mg
答：（1）AB长度得：l=
．
（2）小物体第一次通过C点时对轨道的压力6mg．
解：（1）因恰能过最高点C，则有mg=m| v2 |
| R |
又因f=μN=μmgcosθ，
物体从A运动到C全程，由动能定理
可得：mg（lsinθ-R-Rcosθ）-fl=
| 1 |
| 2 |
联立求得：l=
| ||
| sinθ-μcosθ |
（2）物体从C运动到D的过程，设C点速度为vc，由机械能守恒定律：
| 1 |
| 2 |
| 1 |
| 2 |
物体在C点时：N-mg=
| mvc2 |
| R |
联合求得：N=6mg
答：（1）AB长度得：l=
| ||
| sinθ-μcosθ |
（2）小物体第一次通过C点时对轨道的压力6mg．
点评：本题是动能定理与牛顿运动定律的综合应用，关键是分析物体的运动过程，抓住滑动摩擦力做功与路程有关这一特点．
练习册系列答案
阅读快车系列答案
相关题目
附加题
（2010?济南一模）如图，竖直放置的斜面CD的下端与光滑圆弧轨道ABC的C端相切，圆弧半径为R，圆心与A、D在同一水平面上，∠COB=45°，现将一个质量为m的小物块从A点上方距A竖直高度为h=0.5R的位置无初速释放，小物块从A点进入轨道运动至斜面上D点后返回．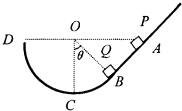
如图，竖直放置的斜面AB的下端与光华圆弧轨道BCD的B端相切，圆弧半径为R，圆心与A、D在同一水平面上，∠COB=θ，现有一个质量为m的小物块P从斜面上的A点无初速滑下，与位于B点的另外一个质量也为m的小物块Q碰撞，碰后，两个物块粘连在一起，已知两个小物块与斜面间的动摩擦因数均为μ，求：