题目内容
 附加题
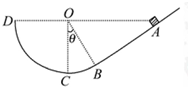
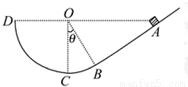
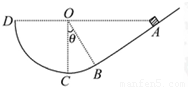
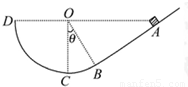
附加题如图,竖直放置的斜面AB的下端与光滑的圆弧轨道BCD的B端相切,C为圆弧最低点,圆弧半径为R,圆心O与A、D在同一水平面上,∠COB=θ.现有一个质量为m的小物体从A点无初速滑下,已知小物体与斜面间的动摩擦因数为μ,求:
(1)小物体在斜面上滑行的总路程;
(2)小物体通过C点时,对C点的最大压力和最小压力.
分析:(1)由几何知识得知,斜面的倾角等于30°.物体从A点无初速度滑下后,由于克服摩擦力做功,物体在斜面上运动时机械能不断减小,到达的最大高度越来越小,最终在BE圆弧上来回运动,到达B点的速度为零.物体在斜面上运动时摩擦力大小为μmgcosθ,总是做负功,滑动摩擦力做的总功与总路程成正比,根据动能定理求解总路程.
(2)当物体第一次经过C点时,速度最大,对C点的压力最大,当最后稳定后,物体在BE之间运动时,经过C点时速度最小,物体对C点的压力最小,根据动能定理求出最大速度和最小速度,再由牛顿运动定律求解最大压力和最小压力.
(2)当物体第一次经过C点时,速度最大,对C点的压力最大,当最后稳定后,物体在BE之间运动时,经过C点时速度最小,物体对C点的压力最小,根据动能定理求出最大速度和最小速度,再由牛顿运动定律求解最大压力和最小压力.
解答:解:(1)设物体在斜面上滑行的总路程为S.对物体从A到B(或E)的过程,应用动能定理得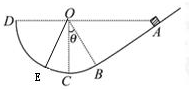
mgRcosθ-μmgcosθS=0
解得 S=
(2)当物体第一次经过C点时,速度最大,设为vC1.由几何知识得到,AB的长度AB=Rcotθ
对A到C过程,由动能定理得
mgR-μmgcosθRcotθ=
m
设轨道对物体的支持力F1,由牛顿第二定律得
F1-mg=m
联立解得F1=3mg-2μmgcosθcotθ
当最后稳定后,物体在BE之间运动时,设物体经过C点的速度为vC2,由动能定理得
mgR(1-cosθ)=
m
设轨道对物体的支持力F2,由牛顿第二定律得
F2-mg=m
联立解得 F2=3mg-2mgcosθ
由牛顿第三定律可知,物体对C点的最大压力为3mg-2μmgcosθcotθ,
最小压力为3mg-2mgcosθ
答:(1)小物体在斜面上滑行的总路程是
;
(2)物体对C点的最大压力为3mg-2μmgcosθcotθ,最小压力为3mg-2mgcosθ.

mgRcosθ-μmgcosθS=0
解得 S=
| R |
| μ |
(2)当物体第一次经过C点时,速度最大,设为vC1.由几何知识得到,AB的长度AB=Rcotθ
对A到C过程,由动能定理得
mgR-μmgcosθRcotθ=
| 1 |
| 2 |
| v | 2 C1 |
设轨道对物体的支持力F1,由牛顿第二定律得
F1-mg=m
| ||
| R |
联立解得F1=3mg-2μmgcosθcotθ
当最后稳定后,物体在BE之间运动时,设物体经过C点的速度为vC2,由动能定理得
mgR(1-cosθ)=
| 1 |
| 2 |
| v | 2 C1 |
设轨道对物体的支持力F2,由牛顿第二定律得
F2-mg=m
| ||
| R |
联立解得 F2=3mg-2mgcosθ
由牛顿第三定律可知,物体对C点的最大压力为3mg-2μmgcosθcotθ,
最小压力为3mg-2mgcosθ
答:(1)小物体在斜面上滑行的总路程是
| R |
| μ |
(2)物体对C点的最大压力为3mg-2μmgcosθcotθ,最小压力为3mg-2mgcosθ.
点评:本题是动能定理与牛顿运动定律的综合应用,关键是分析物体的运动过程,抓住滑动摩擦力做功与路程有关这一特点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目