题目内容
（12分）如图所示，光滑绝缘的细圆管弯成半径为R的半圆形，固定在竖直面内、管口B、C的连线是水平直径，现有一带正电小球（可视为质点）从B点正上方的A点自由下落，A、B两点间距离为4R，从小球进入管口开始，整个空间中突然加上一个匀强电场，电场力在竖直向上的分力大小与重力大小相等，结果小球从管口C处脱离圆管后，其运动轨迹最后经过A点，设小球运动过程中带电量没有改变，重力加速度为g，求：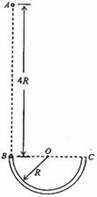
（1）小球到达B点的速度大小；
（2）小球受到的电场力的大小和方向；
（3）小球经过管口C处时对圆管壁的压力。
（1）
（2）
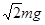（3）
解析试题分析：（1）小球从开始自由下落到到达管口B的过程中机械能守恒，故有：
小球到达B点时的速度大小为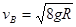
（2）设电场力的水平分力为
（方向水平向左），竖直分力为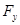
（方向水平向上），则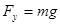
小球从B运动到C的过程中，由动能定理得：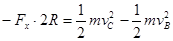
小球从管口C处脱离圆管后，做类平抛运动，由于其轨迹经过A点，有: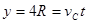
联立以上各式，解得：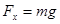
电场力的大小为：
，方向斜向左上方与水平方向夹角450.
（3）小球经过管口C处时，向心力由和圆管的弹力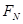
提供，设弹力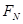的方向向左，则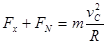
解得：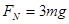
，方向向左
根据牛顿第三定律可知，小球经过管口C处时对圆管的压力为：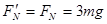
，方向水平向右
考点：本题考查了用功能观点研究带电体在电场中的运动。
练习册系列答案
相关题目
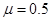，重力加速度g已知。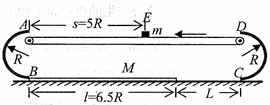
与L的关系.并判断物块能否滑到CD轨道的中点。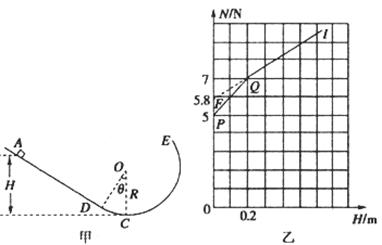
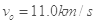的速度时进入地月转移轨道向月球飞去。后6次点火的主要作用是修正飞行方向和被月球捕获时的紧急刹车，最终把卫星送入离月面h=200km高的工作轨道（可视为匀速圆周运动）。已知地球质量是月球质量的81倍，
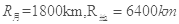，卫星质量为2350kg，地球表面重力加速度
，引力恒量
。(结果保留一位有效数字）求：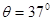
，劲度系数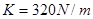
的轻质光滑弹簧平行于传送带放置，下端固定在水平地面上，另一端自由状态时位于Q点。小滑块质量
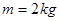，放置于传送带P点，滑块与传送带间的滑动摩擦因数
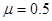。 已知传送带足够长，最大静摩擦力可认为和滑动摩擦力相等， 整个过程中小滑块未脱离传送带，弹簧处于弹性限度内，弹簧的弹性势能
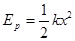，x为弹簧的形变量 (重力加速度g=10m/s2,sin370=0.6,cos370=0.8）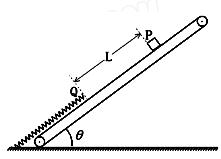
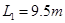，求小物块滑行的最大距离
；
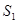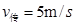速度逆时针传动，将小滑块无初速放在P点， PQ距离
，求小物块滑行的最大距离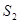
。
，O为轨道的最低点。（g=10m/s2，sin37°=0.6，cos37°=0.8）试求：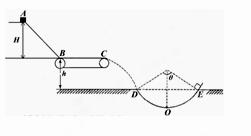
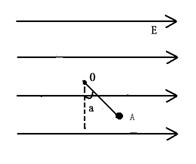
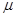=0.20,重力加速度g=10m/s2 ,求：
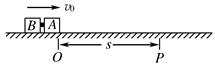
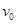一起从O点滑出，滑行一段距离后到达P点，速度变为
，此时炸药爆炸使木块A、B脱离，发现木块B立即停在原位置，木块A继续沿水平方向前进．已知O、P两点间的距离为s，炸药爆炸时释放的化学能均全部转化为木块的动能，爆炸时间很短可以忽略不计．求：