题目内容
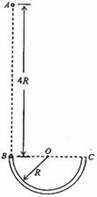
(19分)如图所示,以A、B和C、D为断点的两半圆形光滑轨道固定于竖直平面内,一滑板静止在光滑的地面上,左端紧靠B点,上表面所在平面与两半圆分别相切于B、C两点,一物块(视为质点)被轻放在水平匀速运动的传送带上E点,运动到A点时刚好与传送带速度相同,然后经A点沿半圆轨道滑下,再经B点滑上滑板,滑板运动到C点时被牢固粘连。物块可视为质点,质量为m,滑板质量为M=2m,两半圆半径均为R,板长l=6.5R,板右端到C点的距离L在R<L<5R范围内取值,E点距A点的距离s=5R,物块与传送带、物块与滑板间的动摩擦因数均为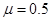 ,重力加速度g已知。
,重力加速度g已知。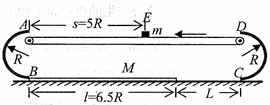
(1)求物块滑到B点的速度大小;
(2)求物块滑到B点时对半圆轨道的压力;
(3)试讨论物块从滑上滑板到离开右端的过程中,克服摩擦力做的功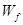 与L的关系.并判断物块能否滑到CD轨道的中点。
与L的关系.并判断物块能否滑到CD轨道的中点。
(1) (2)10mg (3)①R<L<2R时,Wf=
(2)10mg (3)①R<L<2R时,Wf=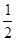 mg(6.5R+L)
mg(6.5R+L)
②2R≤L<5R时,Wf==4.25mgR<4.5mgR,
物块不能滑到CD轨道中点
解析试题分析:(1)设物块滑到B点的速度大小为uB,对物体从E到B过程,
根据动能定理得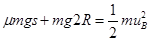 .
.
解得: .
.
(2)物块在B点时,根据牛顿第二定律午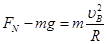 .
.
解得: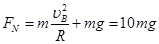 .
.
(3)物块从B滑上滑板后开始作匀减速运动,此时滑板开始作匀加速直线运动,当物块与滑板达共同速度时,二者开始作匀速运动。
由动量定理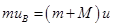
它们的共同速度为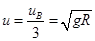
此过程,对物块据动能定理得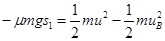 .
.
解得s1=8R .
此过程,对滑板据动能定理得 .
.
解得s2=2R .
由此可知物块在滑板上滑过s1-s2=6R时,二者就具有共同速度了。因为6R<6.5R,所以物块并没有从滑板上滑下去 .
讨论:
?当R<L<2R时,物块在滑板上一直匀减速运动至右端,运动的位移为6.5R+L,克服摩擦力做的功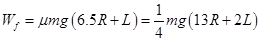 ,
,
设滑上C点的速度为 ,对物块,根据动能定理得:
,对物块,根据动能定理得: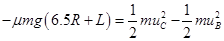 ,
,
解得: 小于mgR,所以物块不可能滑到CD轨道的中点;
小于mgR,所以物块不可能滑到CD轨道的中点;
当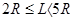 时,物块匀减速运动8R,匀速运动L-2R,再匀减速运动0.5R,克服摩擦力做功
时,物块匀减速运动8R,匀速运动L-2R,再匀减速运动0.5R,克服摩擦力做功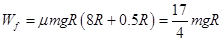 ,
,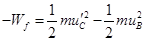
解得 ,所以物块不能滑到CD轨道的中点
,所以物块不能滑到CD轨道的中点
考点:本题考查机械能守恒以及有摩擦的板块模型中克服摩擦力做的功.判断物块与滑板在达到相同共同速度时,物块未离开滑板是关键,是一道比较困难的好题.

 口算题卡北京妇女儿童出版社系列答案
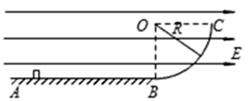
口算题卡北京妇女儿童出版社系列答案 从距O点为
从距O点为 的P点沿斜面向下运动,与弹簧接触后压缩弹簧,将弹簧右端压到O′点位置后,A又被弹簧弹回。A离开弹簧后,恰好回到P点。物块A与斜面间的动摩擦因数为μ,斜面倾角为
的P点沿斜面向下运动,与弹簧接触后压缩弹簧,将弹簧右端压到O′点位置后,A又被弹簧弹回。A离开弹簧后,恰好回到P点。物块A与斜面间的动摩擦因数为μ,斜面倾角为 。求:
。求:

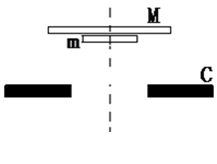
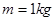 ,半径分别为
,半径分别为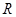 和
和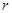 ,两板之间用一根长
,两板之间用一根长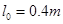 的轻绳将薄板中心相连结(未画出).开始时,两板水平放置并叠合在一起,静止于距离固定支架C高度
的轻绳将薄板中心相连结(未画出).开始时,两板水平放置并叠合在一起,静止于距离固定支架C高度 处. 然后自由下落到C上,支架上有一半径为
处. 然后自由下落到C上,支架上有一半径为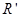 (
(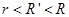 )的圆孔,圆孔与两薄板中心均在圆板中心轴线上. 薄板M与支架发生没有机械能损失的碰撞(碰撞时间极短). 碰撞后,两板即分离,直到轻绳绷紧.在轻绳绷紧的瞬间,两板立即具有共同速度.不计空气阻力,
)的圆孔,圆孔与两薄板中心均在圆板中心轴线上. 薄板M与支架发生没有机械能损失的碰撞(碰撞时间极短). 碰撞后,两板即分离,直到轻绳绷紧.在轻绳绷紧的瞬间,两板立即具有共同速度.不计空气阻力,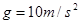 ,求:
,求: