题目内容
如图所示，长为l的轻杆AC可绕A端在竖直平面内无摩擦地转动，在C端和杆上的B处(AB＝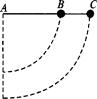
)各固定有质量均为m的小球，现将杆拉到水平位置后从静止释放，求杆的C端到达最低位置时的速度和这一过程中杆的BC段对C球所做的功．
答案：
解析：
提示：
解析：
解析：B、C两球在运动过程中，杆的BC段分别要对它们做功，所以单独对B或C球来说机械能不守恒，但对B、C两球组成的系统来说只有两小球受的重力做功，故系统的机械能守恒．在杆转动的过程中，系统减少的势能转化为其增加的动能．即mg l＋mgl＝ mνB2＋ mνc2，由于二者的角速度相等，故还有νB：νc＝2：3，解以上两式可得νc＝ 对C球由动能定理得WBC＋mgl＝ mνc2-0所以BC段杆对C球做的功为WBC＝ mνC2-mgl＝ m( )2-mgl-mgl＝ mgl．
|
提示：
| 点拨：在涉及有几个物体参与运动的过程，一般先以整体来分析，利用机械能守恒定律及相互间的制约关系求解，在确定系统内作用力做功时，再将它们分开来研究．从本例解的结果可看出，单独的B、C两球机械能不守恒．事实上，AB杆对B球做负功，BC杆对C球做正功．
|
练习册系列答案
快捷英语周周练系列答案
相关题目
（2004?天津模拟）如图所示，长为l的轻杆一端固定一质量为m的小球，另一端有固定转轴O，杆可在竖直平面内绕转轴O无摩擦转动．已知小球通过最低点Q时，速度大小为v=2
如图所示，长为L的轻杆一端固定一个小球，另一端固定在光滑水平轴上，使小球在竖直平面内做圆周运动，设小球在过最高点A点的速度v，下列叙述中正确的是（ ）
如图所示，长为L的轻绳一端固定于O点，另一端系一个小球．现使小球在竖直平面内做圆周运动，P是圆周轨道最高点，Q是轨道最低点．已知重力加速度为g．若小球刚好能够通过最高点P，则以下判断正确的是（ ）
如图所示，长为L的轻杆两端各连一个质量均为m的小球（半径可以忽略不计），以它们的中点为轴，在竖直平面内做匀速圆周运动，转动周期为T=2π
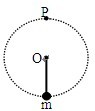如图所示，长为L的轻杆一端固定质量为m的小球，另一端有固定转轴O，现使小球在竖直平面内做圆周运动，P为圆周的最高点，若小球通过圆周轨道最低点时的速度大小为
|
| A、小球不能到达P点 | ||
B、小球到达P点时的速度大于
| ||
| C、小球能到达P点，且在P点受到轻杆向下的拉力 | ||
| D、小球能到达P点，且在P点受到轻杆向上的支持力 |