题目内容

如图所示，竖直面内有一绝缘轨道，AB部分是光滑的四分之一圆弧，圆弧半径R=0.5m，B处切线水平，BC部分为水平粗糙直轨道。有一个带负电的小滑块（可视为质点）从A点由静止开始下滑，运动到直轨道上的P处刚好停住。小滑块的质量m=1kg，带电量为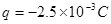保持不变，滑块小轨道BC部分间的动摩擦因数为μ=0.2，整个空间存在水平向右的匀强电场，电场强度大小为E=4.0×102N/C.（g=10m/s2）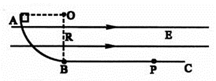

（1）求滑块到达B点瞬间的速度大小
（2）求滑块到达B点瞬间对轨道的压力大小。
（3）求BP间的距离，

（1）3m/s（2）28N（3）1.5m

解析试题分析:
（1）小滑块从A点运动到B点的过程中，弹力不做功，重力做正功，电场力做负功.由动能定理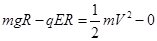
  （2分）
解得 V=3m/s；          （1分）
（2）在B点，小滑块在竖直方向只受重力和支持力的作用，由向心力公式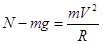
        （2分）
解得：N=28N
由牛顿第三定律得滑块到达B点瞬间对轨道的压力大小N’=28N  （1分）
（2）小滑块从B点运动到P点的过程中，弹力和重力不做功，滑动摩擦力和电场力做负功.由动能定理
     （2分）
解得：x=1.5m        （2分）
考点： 动能定理的应用；向心力公式；牛顿第三定律应用；重力和电场力做功特点；

练习册系列答案
相关题目

（20分）如图所示，水平线QC下方是水平向左的匀强电场；区域Ⅰ（梯形PQCD）内有垂直纸面向里的匀强磁场，磁感应强度为B；区域Ⅱ（三角形APD）内也有垂直纸面向里的匀强磁场，但是磁感应强度大小可以与区域Ⅰ不同；区域Ⅲ（虚线PD之上、三角形APD以外）有垂直纸面向外的匀强磁场，磁感应强度与区域Ⅱ内磁感应大小相等。三角形AQC是边长为2L的等边三角形，P、D分别为AQ、AC的中点．带正电的粒子从Q点正下方、距离Q点为L的O点以某一速度射出，在电场力作用下从QC边中点N以速度v0垂直QC射入区域Ⅰ，接着从P点垂直AQ射入区域Ⅲ。若区域Ⅱ、Ⅲ的磁感应强度大小与区域Ⅰ的磁感应强度满足一定的关系，此后带电粒子又经历一系列运动后又会以原速率返回O点．（粒子重力忽略不计）求：

（1）该粒子的比荷；
（2）粒子从O点出发再回到O点的整个运动过程所有可能经历的时间．

（18分）如图，空间存在匀强电场和匀强磁场，电场方向为y轴正方向，磁场方向垂直于xy平面（纸面）向外，电场和磁场都可以随意加上或撤除，重新加上的电场或磁场与撤除前的一样.一带正电荷的粒子从P（x=0，y=h）点以一定的速度平行于x轴正向入射.这时若只有磁场，粒子将做半径为R0的圆周运动；若同时存在电场和磁场，粒子恰好做直线运动.现在，只加电场，当粒子从P点运动到x=R0平面（图中虚线所示）时，立即撤除电场同时加上磁场，粒子继续运动，其轨迹与x轴交于M点.不计重力.求：

⑴粒子到达x=R0平面时速度方向与x轴的夹角以及粒子到x轴的距离；
⑵M点的横坐标xM.

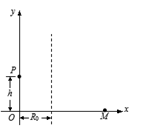
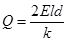（8分）如图所示，相距为d的虚线AB、CD之间存在着水平向左的、场强为E的匀强电场，M、N是平行于电场线的一条直线上的两点，紧靠CD边界的右侧有一O点，与N点相距为l，在O点固定一电荷量为（k为静电力常量）的正点电荷，点电荷产生的电场只存在于CD边界的右侧。今在M点释放一个质量为m、电量为-e的电子（重力不计）。求：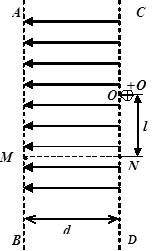

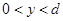（1）电子经过N点时的速度大小。
（2）判断电子在CD右侧做什么运动，并求出电子从M点释放后经过N点的时间。

（14分）坐标原点O处有一点状的放射源，它向xoy平面内的x轴上方各个方向发射α粒子，α粒子的速度大小都是v0，在的区域内分布有指向y轴正方向的匀强电场，场强大小为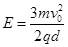，其中q与m分别为α粒子的电量和质量；在的区域内分布有垂直于xoy平面向里的匀强磁场．ab为一块很大的平面感光板，放置于处，如图所示．观察发现此时恰无粒子打到ab板上．（不考虑α粒子的重力）

（1）求α粒子刚进入磁场时的动能；
（2）求磁感应强度B的大小；
（3）将ab板平移到什么位置时所有粒子均能打到板上? 并求出此时ab板上被α粒子打中
的区域的长度．

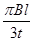（14分）在xOy平面第Ⅰ、Ⅱ象限中，存在沿y轴正方向的匀强电场，场强为E＝，在第Ⅲ、Ⅳ象限中，存在垂直于xOy平面方向的匀强磁场,如图所示,磁感应强度B1＝B，B2＝2B．带电粒子a、b分别从第Ⅰ、Ⅱ象限的P、Q两点（图中没有标出）由静止释放，结果两粒子同时分别进入匀强磁场B1、B2中，再经过时间t第一次经过y轴时恰在点M（0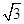，－l）处发生碰撞，碰撞时两粒子的速度在同一直线上，碰撞前带电粒子b的速度方向与y轴正方向成60°角，不计粒子重力和两粒子间相互作用．求：

（1）两带电粒子的比荷及在磁场中运动的轨道半径;
（2）带电粒子释放的位置P、Q两点坐标及释放的时间差．

（16分）为了使粒子经过一系列的运动后，又以原来的速率沿相反方向回到原位，可设计如下的一个电磁场区域（如图所示）：水平线QC以下是水平向左的匀强电场，区域Ⅰ(梯形PQCD)内有垂直纸面向里的匀强磁场，磁感应强度为B；区域Ⅱ(三角形APD)内的磁场方向与Ⅰ内相同，但是大小可以不同，区域Ⅲ(虚线PD之上、三角形APD以外)的磁场与Ⅱ内大小相等、方向相反．已知等边三角形AQC的边长为2l，P、D分别为AQ、AC的中点．带正电的粒子从Q点正下方、距离Q点为l的O点以某一速度射出，在电场力作用下从QC边中点N以速度v0垂直QC射入区域Ⅰ，再从P点垂直AQ射入区域Ⅲ，又经历一系列运动后返回O点．（粒子重力忽略不计）求：

（1）该粒子的比荷．
（2）粒子从O点出发再回到O点的整个运动过程所需时间．

如图所示，两金属杆AB和CD长均为L，电阻均为R，质量分别为3m和m。用两根质量和电阻均可忽略的不可伸长的柔软导线将它们连成闭合回路，并悬挂在水平、光滑、不导电的圆棒两侧。在金属杆AB下方有高度为H的匀强磁场，磁感应强度大小为B，方向与回路平面垂直，此时，CD处于磁场中。现从静止开始释放金属杆AB，经过一段时间，AB即将进入磁场的上边界时，其加速度为零，此时金属杆CD尚未离开磁场，这一过程中杆AB产生的焦耳热为Q。则

（1）AB棒刚达到磁场边界时的速度v1多大？
（2）此过程中金属杆CD移动的距离h和通过导线截面的电量q分别是多少？
（3）通过计算说明金属杆AB在磁场中可能具有的速度大小v2在什么范围内；
（4）试分析金属杆AB在穿过整个磁场区域过程中可能出现的运动情况（加速度与速度的变化情况）。

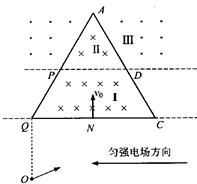
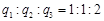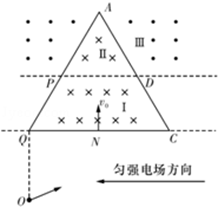
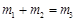如图所示，在xOy坐标系中，第一象限存在一与xOy平面平行的匀强电场，在第二象限存在垂直于纸面的匀强磁场。在y轴上的P点有一静止的带正电的粒子，某时刻，粒子在很短时间内（可忽略不计）分裂成三个带正电的粒子1、2和3，它们所带的电荷量分别为q1、q2和q3，质量分别为m1、m2和m3，且，。带电粒子1和2沿x轴负方向进人磁场区域，带电粒子3沿x轴正方向进入电场区域。经过一段时间三个带电粒子同时射出场区，其中粒子1、3射出场区的方向垂直于x轴，粒子2射出场区的方向与x轴负方向的夹角为60°。忽略重力和粒子间的相互作用。求：

（1）三个粒子的质量之比；
（2）三个粒子进入场区时的速度大小之比；
（3）三个粒子射出场区时在x轴上的位移大小之比。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网