题目内容
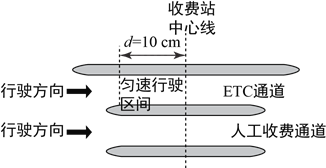
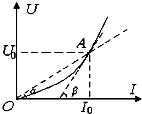
【题目】如图甲所示,电子源能源源不断地产生的电子,电子从电子源飞出时的速度可忽略不计,电子离开电子源后进入一加速电压为U0的加速电场,再沿平行金属板的方向从两板正中间射入偏转电场,当在两板间加如图乙所示的周期为2t0 , 幅值恒为U0的周期性电压时,恰好能使所有电子均从两板间通过.这些电子通过偏转电场的时间为3t0;偏转电场极板右端有足够大的荧光屏(设电子的电荷量为e、质量为m,电子的重力可忽略不计),求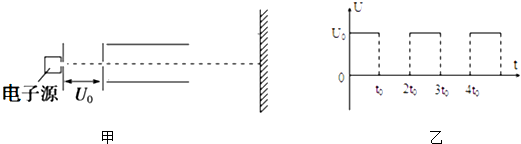
(1)平行金属板的长度l;
(2)平行金属板的间距d;
(3)电子刚到达荧光屏时的最大动能和最小动能之比.
【答案】
(1)解:电子在直线加速过程,有: ![]() ,解得:
,解得: ![]() ;
;
在偏转电场中的水平分运动是匀速直线运动,故:l= ![]() ;
;
答:平行金属板的长度l为 ![]() ;
;
(2)解:恰好能使所有电子均从两板间通过,说明在t=0时刻进入的电子的偏移量为 ![]() ;
;
在t=0时刻进入的电子在0﹣t0时间的竖直分运动是匀加速直线运动,t0﹣2t0时间的竖直分运动是匀速直线运动,t0﹣2t0时间的竖直分运动是匀加速直线运动,故:
![]()
解得:d= ![]() ;
;
答:平行金属板的间距d为 ![]() ;
;
(3)解:电子在t=0时刻进入偏转电场的末动能最大,故: ![]() =
= ![]() ;
;
电子在t=t0时刻进入偏转电场的末动能最小,故: ![]() =
= ![]() ;
;
故 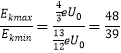 =
= ![]() ;
;
答:电子刚到达荧光屏时的最大动能和最小动能之比16:13.
【解析】(1)(2)对电子的直线加速过程运用动能定理列式求解末速度;在偏转电场中,水平分运动是匀速直线运动,竖直分运动是变速运动,根据分运动公式列式分析;(3)粒子在偏转电场中的竖直分运动是变速运动,采用运动的合成分解法求解末动能表达式分析.
【考点精析】认真审题,首先需要了解带电微粒(计重力)在电场中的运动(带电颗粒:如液滴、油滴、尘埃、小球等,除有说明或明确的暗示以外,一般都不能忽略重力;由于带电粒子在匀强电场中所受电场力与重力都是恒力,因此可以用两种方法处理:①正交分解法;②等效“重力”法).