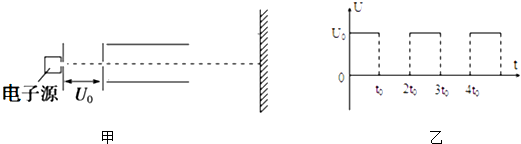Question

【题目】如图所示，a点距坐标原点的距离为L，坐标平面内有边界过a点和坐标原点0的圆形匀强磁场区域，磁场方向垂直坐标平面向里．有一电子（质量为m、电荷量为e）从a点以初速度v0平行x轴正方向射入磁场区域，在磁场中运行，从x轴上的b点（图中未画出）射出磁场区域，此时速度方向与x轴的正方向之间的夹角为60°，求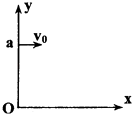

（1）磁场的磁感应强度
（2）磁场区域的圆心O1的坐标
（3）电子在磁场中运动的时间．

Answer 1

【答案】
（1）解：粒子运动的轨迹如图得R=2L

又，洛伦兹力提供向心力，得：

所以：

答：磁场的磁感应强度 ；

（2）解：由题意和上图的几何关系可得，过a、O、B三点的圆的圆心在aB连线的中点．所以：

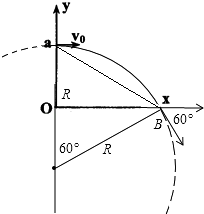
x轴坐标x=aO1sin60°=

y轴坐标为y=L﹣aO1sin60°=

O1点坐标为（ ）

答：磁场区域的圆心O1的坐标（ ）

（3）解：粒子在磁场中飞行时间为：

答：电子在磁场中运动的时间 ．

【解析】（1）根据题意正确画出粒子运动的轨迹，找出R与L之间的关系，由洛伦兹力提供向心力的方程可得；（2）由题意和上图的几何关系可得，过a、O、B三点的圆的圆心在aB连线的中点；（3）粒子在磁场中飞行时间为弧度比速度．
【考点精析】利用洛伦兹力对题目进行判断即可得到答案，需要熟知洛伦兹力始终垂直于v的方向，所以洛伦兹力一定不做功．