题目内容
如图3所示,一质量为m的小球,在B点从静止开始沿半球形容器内壁无摩擦地滑下,B点与容器底部A点的高度差为h.容器质量为M,内壁半径为R,求:
(1)当容器固定在水平桌面上,小球滑至底部A时,容器内壁对小球的作用力大小.
(2)当容器放置在光滑的水平桌面上,小球滑至底部A时,小球相对容器的速度大小?容器此时对小球的作用力大小.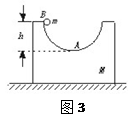
(1)当容器固定在水平桌面上,小球滑至底部A时,容器内壁对小球的作用力大小.
(2)当容器放置在光滑的水平桌面上,小球滑至底部A时,小球相对容器的速度大小?容器此时对小球的作用力大小.

(1)T=mg+m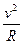 =mg+m
=mg+m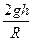 =mg(1+
=mg(1+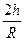 )
)
(2)v′=v1-v2=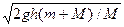
T′=mg+m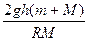 =mg[1+
=mg[1+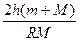 ]
]
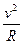 =mg+m
=mg+m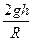 =mg(1+
=mg(1+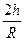 )
)(2)v′=v1-v2=
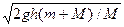
|
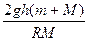 =mg[1+
=mg[1+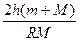 ]
] (1)m下滑只有重力做功,故机械能守恒,即有
mgh= mv2,v2=2gh ①
mv2,v2=2gh ①
底部A是圆周上的一点,由牛顿第二定律,有:T-mg=m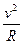
T=mg+m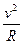 =mg+m
=mg+m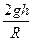 =mg(1+
=mg(1+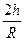 )
)
(2)容器放置在水平桌面上,则m与M组成的系统在水平方向不受外力,故系统在水平方向上动量守恒;又因m与M无摩擦,故m与M的总机械能也守恒.令m滑到底部时,m的速度为v1,M的速度为v2.
由动量守恒定律得:0=mv1+Mv2 ①
由机械能守恒定律得:mgh= mv12+
mv12+ Mv22 ②
Mv22 ②
联立①②两式解得:v1=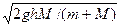 ,v2=-
,v2=-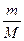
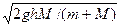
小球相对容器的速度大小v′,v′=v1-v2=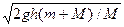
由牛顿第二定律得:T′-mg=m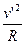
T′=mg+m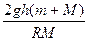 =mg[1+
=mg[1+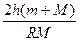 ]
]
mgh=
 mv2,v2=2gh ①
mv2,v2=2gh ①底部A是圆周上的一点,由牛顿第二定律,有:T-mg=m
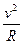
T=mg+m
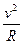 =mg+m
=mg+m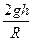 =mg(1+
=mg(1+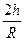 )
)(2)容器放置在水平桌面上,则m与M组成的系统在水平方向不受外力,故系统在水平方向上动量守恒;又因m与M无摩擦,故m与M的总机械能也守恒.令m滑到底部时,m的速度为v1,M的速度为v2.
由动量守恒定律得:0=mv1+Mv2 ①
由机械能守恒定律得:mgh=
 mv12+
mv12+ Mv22 ②
Mv22 ②联立①②两式解得:v1=
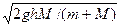 ,v2=-
,v2=-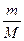
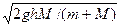
小球相对容器的速度大小v′,v′=v1-v2=
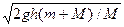
由牛顿第二定律得:T′-mg=m
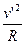
T′=mg+m
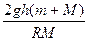 =mg[1+
=mg[1+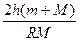 ]
]
练习册系列答案
相关题目
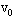 =800m/s射入木块后留在木块中,当木块与前方距离较远的竖直墙碰后,以4m/s的速度反弹回,木块与墙的作用时间为0.1s
=800m/s射入木块后留在木块中,当木块与前方距离较远的竖直墙碰后,以4m/s的速度反弹回,木块与墙的作用时间为0.1s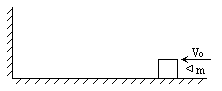
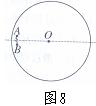
 光滑圆弧的质量为M的曲面体,已知曲面顶端切线竖直。若M未能越过曲面体,求球到达最高点时曲面体的速度以及曲面半径的最小值。
光滑圆弧的质量为M的曲面体,已知曲面顶端切线竖直。若M未能越过曲面体,求球到达最高点时曲面体的速度以及曲面半径的最小值。
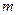 带电荷量为
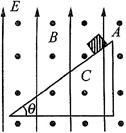
带电荷量为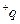 的小滑块静止在斜面顶端时对斜面的正压力恰好为零,如图所示。
的小滑块静止在斜面顶端时对斜面的正压力恰好为零,如图所示。 ;
;

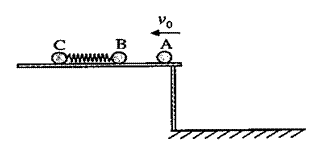
 停放着一辆质量M=6.0kg平板车,在车上左端放有一质量mB=4.0kg木块B。车左边紧邻一个与平板车等高的光滑水平面,现有另一质量mA= 2.0kg的木块A,从左侧光滑水平面上以v0=3.0m/s向右运动,然后与B发生碰撞,设木块A、B碰撞时间很短且为弹性正碰。碰后木块B开始在平板车上滑行,并与固定在平板车上的水平轻质弹簧作用后与弹簧分离,已知木块B把弹簧压缩到最短时距离平板车左侧的距离为L=0.20m,重力加速度为g=10m/s2,木块B与平板车之间的动摩擦因数为μ=0.50。(结果保留两位有效数字)求:
停放着一辆质量M=6.0kg平板车,在车上左端放有一质量mB=4.0kg木块B。车左边紧邻一个与平板车等高的光滑水平面,现有另一质量mA= 2.0kg的木块A,从左侧光滑水平面上以v0=3.0m/s向右运动,然后与B发生碰撞,设木块A、B碰撞时间很短且为弹性正碰。碰后木块B开始在平板车上滑行,并与固定在平板车上的水平轻质弹簧作用后与弹簧分离,已知木块B把弹簧压缩到最短时距离平板车左侧的距离为L=0.20m,重力加速度为g=10m/s2,木块B与平板车之间的动摩擦因数为μ=0.50。(结果保留两位有效数字)求:
