题目内容
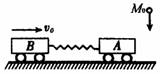
如图所示,质量为3m的足够长木板C 静止在光滑水平面上,质量均为m 的两个物体A、B 放在C 的左端,A、B 间相距s0,现同时对A、B施加水平向右的瞬间冲量而使之分别获得初速度v0和2v0,若A、B与C之间的动摩擦因数分别为μ 和 2 μ ,则:
(1)最终A、B、C的共同速度为多大
(2)求A达到最小速度时,系统产生的热量Q。
(1)最终A、B、C的共同速度为多大
(2)求A达到最小速度时,系统产生的热量Q。

(1)v共=0.6v0
(2)Q=1.5mv02
(2)Q=1.5mv02
】(1)对A、B、C组成的系统,最终相对静止,设共同速度为v共,由动量守恒定律:
mv0+2mv0=(m+m+3m)v共
解得:v共=0.6v0
(2)A、B相对C向右匀减速运动阶段,C做匀加速运动,设A的加速度为aA,B的加速度为aB,C的加速度为aC ,设t时刻A、C达到共同速度vA,B的速度为vB
由牛顿第二定律:
aA=gμ
aB=2gμ
aC=gμ
t时间内,对A,由速度公式:vA=v0-aAt
对B:vB=2v0-aBt
对C:vA=aC t
解得:vA=0.5v0
vB=v0
此后A、C一起匀加速运动,B继续以加速度aB减速运动,故运动过程中A的最小速度为vA=0.5v0
根据系统的能量守恒定律,系统产生的热量
Q=mv02+m(2v0)2-mvA2-×3mvA2-mvB2
解得Q=1.5mv02
mv0+2mv0=(m+m+3m)v共
解得:v共=0.6v0
(2)A、B相对C向右匀减速运动阶段,C做匀加速运动,设A的加速度为aA,B的加速度为aB,C的加速度为aC ,设t时刻A、C达到共同速度vA,B的速度为vB
由牛顿第二定律:
aA=gμ
aB=2gμ
aC=gμ
t时间内,对A,由速度公式:vA=v0-aAt
对B:vB=2v0-aBt
对C:vA=aC t
解得:vA=0.5v0
vB=v0
此后A、C一起匀加速运动,B继续以加速度aB减速运动,故运动过程中A的最小速度为vA=0.5v0
根据系统的能量守恒定律,系统产生的热量
Q=mv02+m(2v0)2-mvA2-×3mvA2-mvB2
解得Q=1.5mv02

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
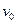 开始运动,并与固定在木板另一端的弹簧相碰后返回,恰好又停在木板左端,求:
开始运动,并与固定在木板另一端的弹簧相碰后返回,恰好又停在木板左端,求: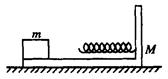
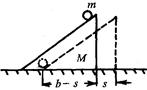
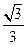 倍,电场范围足够大,在距O点为L的正下方有另一完全相同的不带电的金属小球B置于光滑绝缘水平桌面的最左端,桌面离地距离为H,现将细线向右水平拉直后从静止释放A球。
倍,电场范围足够大,在距O点为L的正下方有另一完全相同的不带电的金属小球B置于光滑绝缘水平桌面的最左端,桌面离地距离为H,现将细线向右水平拉直后从静止释放A球。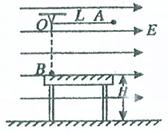
 。则B球落地时的速度大小是多少?(不计碰撞过程中机械能损失及小球间库仑力的作用)
。则B球落地时的速度大小是多少?(不计碰撞过程中机械能损失及小球间库仑力的作用) 的粘性物体,从高处自由下落,正好落至A车并与之粘合在一起,在此后的过程中,弹簧获得最大弹性势能为E,试求A、B车开始匀速运动的初速度
的粘性物体,从高处自由下落,正好落至A车并与之粘合在一起,在此后的过程中,弹簧获得最大弹性势能为E,试求A、B车开始匀速运动的初速度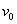 的大小.
的大小.