题目内容
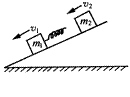
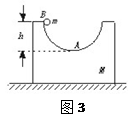
光滑的水平面上,质量为m的小球以速度v0冲上静止放置的带有 光滑圆弧的质量为M的曲面体,已知曲面顶端切线竖直。若M未能越过曲面体,求球到达最高点时曲面体的速度以及曲面半径的最小值。
光滑圆弧的质量为M的曲面体,已知曲面顶端切线竖直。若M未能越过曲面体,求球到达最高点时曲面体的速度以及曲面半径的最小值。

 光滑圆弧的质量为M的曲面体,已知曲面顶端切线竖直。若M未能越过曲面体,求球到达最高点时曲面体的速度以及曲面半径的最小值。
光滑圆弧的质量为M的曲面体,已知曲面顶端切线竖直。若M未能越过曲面体,求球到达最高点时曲面体的速度以及曲面半径的最小值。
h=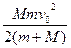
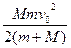
小球到达最高点时与曲面体有共同的速度v对小球的上冲过程,由水平方向动量守恒,得
mv0=(M+m)v 得小球到达最高点时的曲面体的速度为v =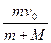
设小球上升的最大高度为h,对这一过程,由机械能守恒得
mgh=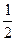 mv02-
mv02-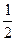 (M+m)v2
(M+m)v2
得球上升的最大高度为h=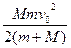 ,此即曲面半径的最小值。
,此即曲面半径的最小值。
mv0=(M+m)v 得小球到达最高点时的曲面体的速度为v =
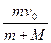
设小球上升的最大高度为h,对这一过程,由机械能守恒得
mgh=
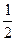 mv02-
mv02-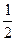 (M+m)v2
(M+m)v2得球上升的最大高度为h=
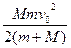 ,此即曲面半径的最小值。
,此即曲面半径的最小值。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

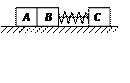

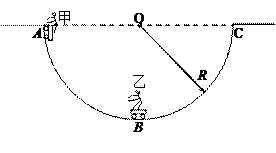
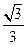 倍,电场范围足够大,在距O点为L的正下方有另一完全相同的不带电的金属小球B置于光滑绝缘水平桌面的最左端,桌面离地距离为H,现将细线向右水平拉直后从静止释放A球。
倍,电场范围足够大,在距O点为L的正下方有另一完全相同的不带电的金属小球B置于光滑绝缘水平桌面的最左端,桌面离地距离为H,现将细线向右水平拉直后从静止释放A球。
 。则B球落地时的速度大小是多少?(不计碰撞过程中机械能损失及小球间库仑力的作用)
。则B球落地时的速度大小是多少?(不计碰撞过程中机械能损失及小球间库仑力的作用)