Question

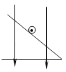
【题目】如图所示，一束平行光以45°的入射角照射到半圆柱形玻璃砖的上表面上，已知玻璃砖对该平行光的折射率为。

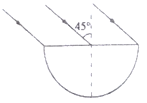
（ⅰ）圆柱面上光线能够射出的区域所对的圆心角θ是多少?

（ⅱ）若用该光进行双缝干涉实验，测得双缝间距为d=0.3mm，双缝到光屏的距离为L=1.2m，第1条亮条纹到第10条亮条纹间的距离为a=22.77mm,求该光的波长。

Answer 1

【答案】(i) 90° (ii) 6.325×10-7 m

【解析】(i)如图1所示，设左侧某束光线经过半圆柱形玻璃砖的上表面再照到其圆柱面时刚好发生全反射，这时光线进入半圆柱形玻璃砖的上表面的入射角为i=45°，折射角为θ，全反射临界角为C，则

n=

解得θ=30° sin C= 解得C=45° 由几何关系可知α=75°

如图2所示，设右侧某束光线经过半圆柱形玻璃砖的上表面再照到其圆柱面时刚好发生全反射，由几何关系可知β=165°

所以光线能够射出圆柱面的区域所对的圆心角θ=β-α=90°

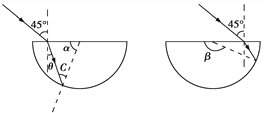
　 　图1　　　　　　　　　图2

(ii) 相邻两条亮条纹间的距离为

Δx= =2.53×10-3 m

根据公式Δx=λ

得λ=Δx=6.325×10-7 m